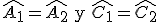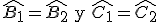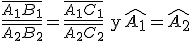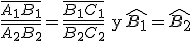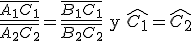1.1. Teorema de Tales. Semejanza de triángulos. Teorema de Pitágoras

El teorema de Tales está presente en infinidad de disciplinas científicas y es un teorema fundamental de la geometría. Durante siglos ha inspirado a múltiples matemáticos. Con este video te mostramos cómo ha servido de inspiración en disciplinas tan diversas como la música.

Actividad

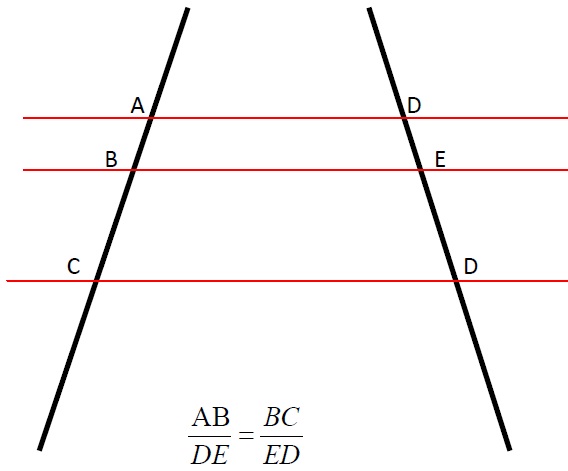Teorema de Tales

Cuando varias rectas paralelas cortan a dos rectas cualesquiera, los segmentos determinados por las paralelas en una de las rectas son proporcionales a los segmentos determinados en la otra recta por las mismas paralelas.

Importante

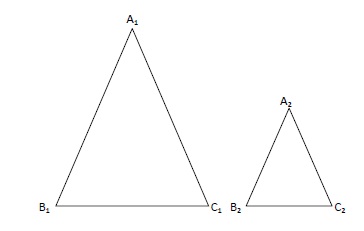
Triángulos semejantes

Dos triángulos son semejantes si todos sus ángulos son iguales y sus lados proporcionales dos a dos, es decir atendiendo a los triángulos del dibujo, ambos triángulos son semejantes si:

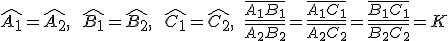
$\widehat{A_1}=\widehat{A_2}, \ \ \widehat{B_1}=\widehat{B_2}, \ \ \widehat{C_1}=\widehat{C_2}, \ \ \frac{\overline{A_1B_1}}{\overline{A_2B_2}}=\frac{\overline{A_1C_1}}{\overline{A_2C_2}}=\frac{\overline{B_1C_1}}{\overline{B_2C_2}}= K$

Donde 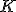es la razón de semejanza entre ambos triángulos

Pero para determinar si dos triángulos son semejantes no es necesario comprobar que los tres ángulos son iguales y que los tres lados son proporcionales dos a dos. Para ello basta con aplicar unos de los tres criterios de semejanza fundamentados en el teorema de Tales.

Importante

Criterios de semejanza

Criterio 1

Dos triángulos son semejantes si dos de sus ángulos son iguales.

Atendiendo a los triángulos anteriores, para demostrar que son semejantes aplicando el criterio 1 bastaría con comprobar:

$\widehat{A_1}=\widehat{A_2} \begin{verbatim} y \end{verbatim} \widehat{B_1}=\widehat{B_2}$

Criterio 2

Dos triángulos son semejantes si sus lados son proporcionales dos a dos, es decir, en los triángulos anteriores si se cumple:

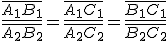
Criterio 3

Dos triángulos son semejantes si dos de sus lados son proporcionales y el ángulo comprendido entre ellos igual.

Atendiendo a los triángulos anteriores, para demostrar que son semejantes aplicando el criterio 1 bastaría con comprobar:

$\frac{\overline{A_1B_1}}{\overline{A_2B_2}}=\frac{\overline{A_1C_1}}{\overline{A_2C_2}} \begin{verbatim} y \end{verbatim}$

Importante

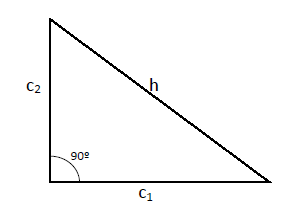Teorema de Pitágoras

Dado cualquier triángulo rectángulo la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado:

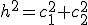
Reflexión

Razona si los siguientes triángulos son semejantes. En caso afirmativo explica en el criterio en el que te basas:

Del primer triángulo conocemos los ángulos 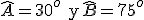$\widehat{A}=30^o \begin{verbatim} y \end{verbatim} \widehat{B}=75^o$ y del segundo conocemos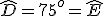
Del primer triángulo conocemos 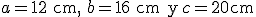$a = 12 \begin{verbatim} cm, \end{verbatim} b = 16 \begin{verbatim} cm y \end{verbatim} c = 20 \begin{verbatim} cm\end{verbatim}$ y del segundo conocemos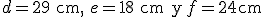 $d = 29 \begin{verbatim} cm, \end{verbatim} e = 18 \begin{verbatim} cm y \end{verbatim} f = 24 \begin{verbatim} cm\end{verbatim}$
El primer triángulo es rectángulo y los catetos miden 6cm y 8 cm y el segundo también es rectángulo uno de los catetos mide 9cm y la hipotenusa mide 15cm.

Retroalimentación

Los dos primeros triángulos son semejates aplicando el criterio 1. Si en el primer triángulo los ángulos miden $\widehat{A}=30^o \begin{verbatim} y \end{verbatim} \widehat{B}=75^o$ y la suma de los ángulos de un triángulo tiene que valer 180º significa que $\widehat{C}=75^o$ . Por lo tanto se cumple el critetio 1 porque ambos triángulos tienen dos ángulos iguales.
Los triángulos de este apartado no son semejantes porque no se cumple el criterio 2 porque $\frac{3}{2}=\frac{e}{a}=\frac{f}{b} eq\frac{d}{c}$
Con los datos de los que disponemos en este apartado se puede asegurar que los triángulos se semejantes por el criterio 1 y por el criterio 3

Si aplicamos el teorema de Pitágoras en el primer triángulo la hipotenusa vale 10cm y en el segundo triángulo el otro cateto vale 12cm por tanto:

Aplicando el criterio 1 los tres lados son proporcionales $\frac{9}{6}=\frac{12}{8}=\frac{15}{10}$
Aplicando el criterio 3 dos de sus lados son proporcionales, en este caso los catetos $\frac{9}{6}=\frac{12}{8}$ , y el ángulo que forman es igual, el ángulo recto.

Reflexión

En un triángulo rectángulo, un cateto tiene la mitad de longitud que el otro, sabiendo que la hipotenusa mide 10 cm. ¿Cuál es el valor de los catetos?

Pregunta de Elección Múltiple

Pregunta

Dado un triángulo rectángulo del que conocemos que los catetos miden 3 cm y 4 cm podemos decir que es semejante a:

Respuestas

Opción 1

Un triángulo del que conocemos que dos de su lados miden 6 cm y 8 cm.

Opción 2

Un triángulo rectángulo del que conocemos que uno de sus catetos mide 6 cm y la hipotenusa 10 cm.

Opción 3

Un triángulo rectángulo isósceles

Retroalimentación

Incorrecto.

No podemos asegurar que sean semejantes porque aunque los lados que conocemos son proporcionales nos faltaría conocer el tercer lado del triángulo.

Correcto.

Aunque a priori no guardan relación los lados por ser ambos rectángulos, aplicando el teorema de Pitágoras podemos calcular los lados que nos faltan. En el triángulo del enunciado podemos calcular que la hipotenusa mide 5 cm. Del mismo modo podemos calcular el cateto que nos falta y saber que su longitud mide 8 cm por lo que ambos triángulos son semejantes por el criterio 2.

Incorrecto.

No es posible que sean semejantes porque al ser este triángulo isósceles significa que los catetos son iguales por tanto no pueden ser proporcionales a los lados del triángulo de partida.

Pregunta

Determina cuales de los siguientes tipos de triángulos no son semejantes entre sí:

Respuestas

Opción 1

Dos triángulos equiláteros cualesquiera.

Opción 2

Dos triángulos rectángulos isósceles cualesquiera.

Opción 3

Dos triángulos isósceles cualesquiera.

Retroalimentación

Incorrecto.

Los triángulos equilateros son semejantes entre sí porque cumplen el criterio 1: Dos de sus ángulos son iguales.

Incorrecto.

Los triángulos rectángulos isósceles son semejantes entre sí por el criterio 3. Tienen un ángulo igual, que es el ángulo recto, y los lados que lo forman, que son los catetos y que son iguales por ser los triángulos isósceles, proporcionales.

Correcto.

Los triángulos isósceles, en general, no son semejantes entre si. Dos de sus lados si son proporcionales por ser ambos isósceles pero del tercero no podemos asegurar que haya proporción.

Solution

Incorrecto (Retroalimentación)
Incorrecto (Retroalimentación)
Opción correcta (Retroalimentación)