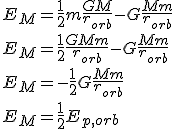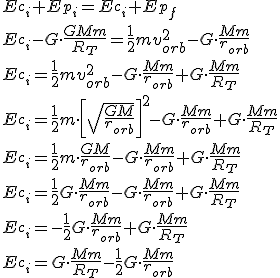3. Estudio de la energía
 |
En este apartado vamos a estudiar la energía de nuestro sistema, un satélite en órbita.
La energía que tendrá el satélite en su órbita viene dada por la expresión de la energía mecánica que no es más que la suma de los dos tipos de energía que ya conocemos: cinética y potencial.
Como conocemos el valor de la velocidad orbital, la expresión anterior nos queda de la siguiente manera:
La ecuación anterior nos da el valor de la energía que un satélite tiene en una órbita específica.
Imagen de NASAvia Wikimedia Commons de dominio público
Es posible conocer también la energía de puesta en órbita: es la energía necesaria transmitir al satélite para ponerlo en órbita. Se determina aplicando de nuevo el principio de conservación de la energía mecánica comparando la posición inicial sobre la superficie de la Tierra(RT) y la posición final a la altura de la órbita, es decir, .
Importante
Como la energía mecánica es constante se deduce que la velocidad y su posición están relacionadas, de forma que cuanto más alejado se encuentre el cuerpo mayor será la energía potencial almacenada, menor por tanto será su energía cinética y con esto su velocidad (coincide con lo estudiado con las leyes de Kepler).
Reflexión
¿Se podría calcular la velocidad con la que hay que lanzar un satélite desde la Tierra para llegar a ponerlo en órbita?
Caso práctico
 Imagen en FLICKR de Jason Major bajo licencia CC |
La agencia espacial desea colocar un satélite de apoyo a la estación orbital internacional para las comunicaciones de masa igual a 200 kg en una órbita por encima de la superficie terrestre de 48 km de altura.
Establece la energía del satélite en esa órbita
Determina la velocidad necesaria para alcanzar la órbita
Datos: g = 9,8 m/s; RT = 6,4·106 m