En el apartado anterior hemos visto como a partir de dos conjuntos A y B podíamos realizar algunas operaciones con ellos como la intersección A ∩ B, la unión A U B o la diferencia o resta A - B. En esta sección vamos a definir una nueva operación entre conjuntos, la multiplicación A x B, que dará lugar a uno de los principios de conteo más usado. 

Veamos cómo se realiza esta operación.

Producto de dos conjuntos

Sean los conjuntos A y B, se define el producto A x B como el conjunto formado por todas las parejas de elementos que podemos formar con un elemento de A y otro de B. Es decir, A x B = { (x, y) tales que x ∈ A e y ∈ B} 

Para aclarar ideas, veamos un ejemplo.

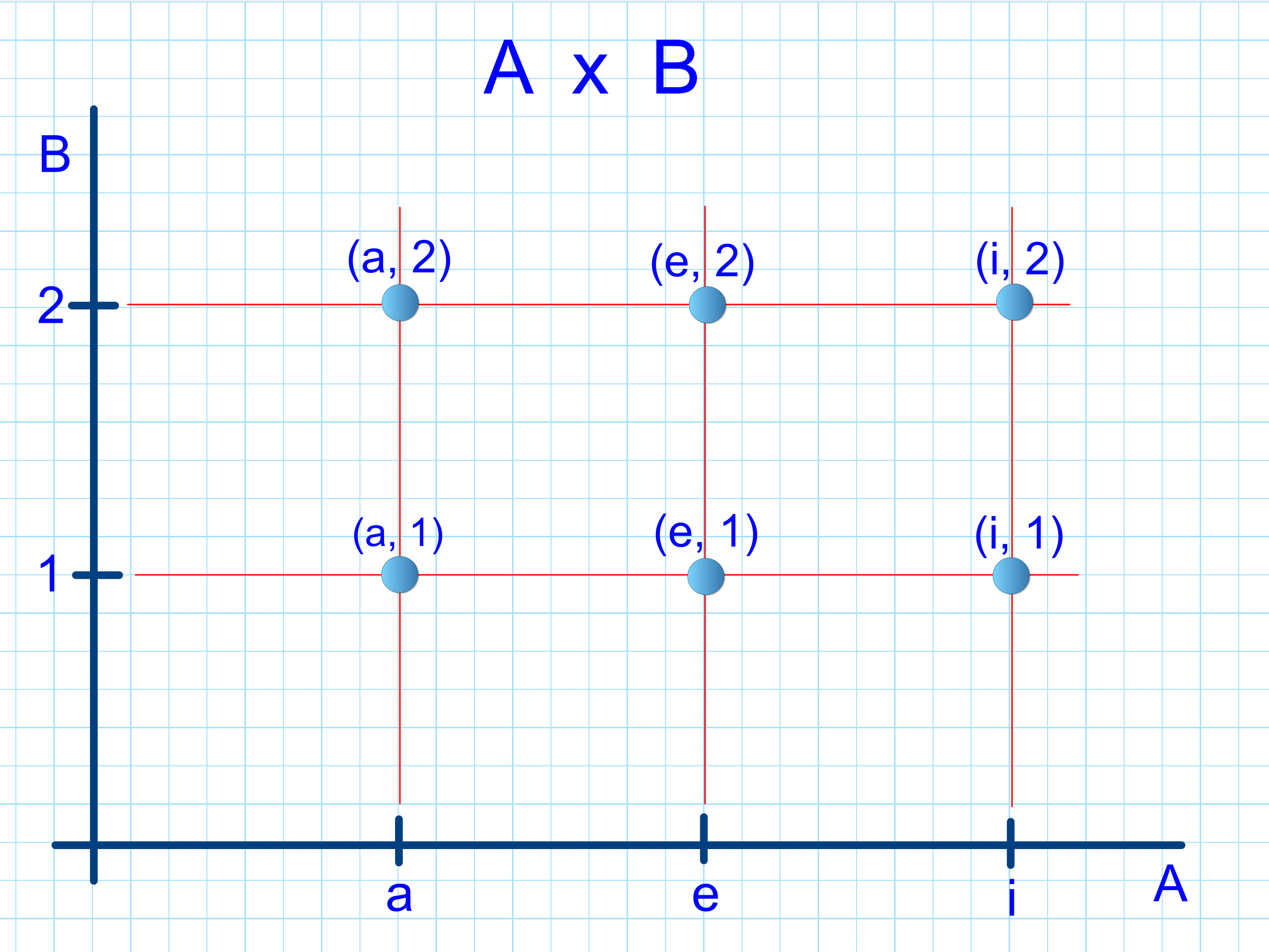
Supongamos que A y B son los conjuntos  A = {a, e, i}  y   B={1, 2}.  Entonces, el producto A x B = { (a, 1), (a, 2), (e, 1), (e, 2), (i, 1), (i, 2) }. En matemáticas, estas parejas de elementos expresadas entre paréntesis y separadas por una coma, recibe el nombre de par ordenado ya que está formado por dos elementos y estos están ordenados, pues primero escribimos el elemento de A y luego el de B. 

Sin embargo, si calculamos B x A, los pares ordenados están invertidos en orden, es decir, B x A = { (1, a), (2, a), (1, e), (2, e), (1, i), (2, i) }. 

A este producto de conjuntos también se le suele llamar producto cartesiano de conjuntos porque sus elementos se pueden representar en un sistema de ejes cartesianos. Veámoslo. 

Existe otra forma de representar el producto de conjuntos llamada Diagrama árbol.

Consiste en colocar los elementos del conjunto A separados y alineados verticalmente.  A continuación, se colocan en la misma disposición los elementos del conjunto B a la derecha de cada elemento de A. Es decir, debemos escribir todos los elementos de B para cada elemento de A. Finalmente, se une mediante una línea (rama) cada elemento del conjunto A con cada uno de los elemento de B tal y como se muestra en la imagen inferior izquierda.  Los elementos del producto se obtienen al emparejar los elementos de A y B  conectados por una rama.  

Esta forma de representar el producto (diagrama árbol) facilita extender esta operación para tres o más conjuntos. El aspecto que adopta esta forma de distribuir los elementos recuerda a las ramas de un árbol que, a su vez, se dividen en otras ramas, de ahí el nombre que recibe. En la imagen superior derecha se muestra el diagrama árbol correspondiente al producto de los tres conjuntos A = {a, e, i}  y   B={1, 2}   y C = {i, u} cuyo resultado es A x B x C = { (a, 1, i), (a, 1, u), (a, 2, i), (a, 2, u), (e, 1, i), (e, 1, u), (e, 2, i), (e, 2, u), (i, 1, i), (i, 1, u), (i, 2, i), (i, 2, u) }. 

Como puede observarse no hay inconveniente en que haya un elemento repetido en dos de los conjuntos, porque lo importante es el orden del producto. Así pues, no hay problema en que el elemento "i" pertenezca al mismo tiempo a los conjuntos A y C, que en cada caso estará en su lugar correspondiente y formará la terna (tres elementos ordenados) correspondiente.

En general, el cardinal del producto de varios conjuntos es igual al producto de sus cardinales. Si tenemos cuatro conjuntos A, B, C y D, el cardinal del producto de todos ellos es igual a:

card(A x B x C x D) = card(A) x card(B) x card(C) x card(D).