Supongamos que una academia de idiomas imparte clases de francés, inglés y alemán. Llamaremos U el conjunto formado por todo su alumnado .

Sobre este conjunto podemos establecer tres subconjuntos: el formado por el alumnado matriculado en francés, el matriculado en inglés y el matriculado en alemán. Vamos a nombrar estos subconjuntos como F, I y A, respectivamente.

Cabe la posibilidad de que algunos alumnos se hayan matriculado en más de un idioma. Por consiguiente, podemos crear unos nuevos conjuntos como, por ejemplo, el formado por el alumnado matriculado en francés e inglés, o en inglés y alemán, o en los tres idiomas. También podemos considerar el formado por el alumnado  matriculado en francés o alemán.

Estos conjuntos se expresan mediante las operaciones de intersección y unión de conjuntos. Veamos cómo se definen.

Intersección de conjuntos

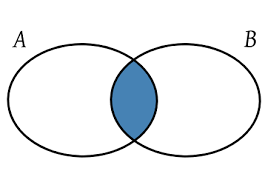
Dados dos conjuntos A y B, la intersección A ∩ B es el conjunto formado por aquellos elementos que pertenecen a ambos conjuntos, $A \cap B = \{ x\ tales\ que\ x \in A \wedge x \in B \}$, es decir, x pertenece a A y x pertenece a B. En la imagen de la derecha, la región sombreada representa la intersección, pues está dentro del conjunto A y también dentro de B (pertenece a ambos). Es importante hacer notar que A ∩ B y B ∩ A representan al mismo conjunto, no importa cual se nombre primero porque la intersección tiene la propiedad conmutativa.

En el ejemplo anterior, el subconjunto formado por el alumnado matriculado en francés e inglés se expresaría F ∩ I y se lee F intersección I.

Y la expresión F ∩ I ∩ A representa el conjunto formado por el alumnado matriculado en los tres idiomas (francés, inglés y alemán).

Unión de conjuntos

Dados dos conjuntos A y B, la unión A U B es el conjunto formado por aquellos elementos que pertenecen al menos a uno de los conjuntos, $A∪B=\left\{x\ tales\ que\ \ x∈A\ o\ x∈B\right\}$, es decir, x pertenece a A o x pertenece a B. En la imagen de la derecha, la región sombreada representa la unión, pues abarca todo el conjunto A y el conjunto B. Es importante hacer notar que A U B y B U A representan al mismo conjunto, no importa cual se nombre primero porque la unión tiene la propiedad conmutativa.

En el ejemplo de la academia, el conjunto formado por el alumnado matriculado en francés o alemán se expresaría F U A, y se lee F unión A.

Observa que U es la unión de los tres subconjuntos F, I y A, es decir, U= F U I U A pues el alumnado está matriculado en, al menos, uno de estos idiomas.

En los ejercicios resueltos 3 y 4, verás, a través de un ejemplo,  cómo se realizan estas operaciones, pero antes de eso, fíjate bien en el siguiente apartado, que se comenta algo muy importante.

Definimos el conjunto complementario de A, y lo representamos por A', al conjunto formado por todos los elementos que no pertenecen a A, es decir, A' = { x tales que x ∉ A}

En algunos textos puedes encontrar este conjunto complementario usando otras notaciones: $ \bar{A}  \    o  \      A^{C}$.

En la imagen de la derecha,  A' se corresponde con la zona sombreada. U representa el conjunto Universal.

Por ejemplo, supongamos U = {a , e, i, o, u} y A = {a, e}, entonces el conjunto complementario de A sería A' = {i, o, u}.

Si tenemos dos conjuntos A y B, definimos la diferencia de conjuntos A - B como el conjunto formado por los elementos de A que no pertenecen a B, es decir, A - B = { x tales que x ∈ A  y  x ∉ B}.

De manera análoga se define B - A como el conjunto formado por los elementos de B que no pertenecen a A.

En este caso, la diferencia de conjuntos no tiene la propiedad conmutativa y no coincidirán los conjuntos diferencia A - B y B - A.

Por ejemplo, si A = { a, e, i} y B = {i, o, u}, entonces A - B = {a, e}  y  B - A = {o, u}