3. La función afín
Estas funciones son también rectas, pero se diferencian de las anteriores en que no pasan por el origen de coordenadas. Pero tú ya conoces algunas funciones de estas ¿recuerdas el teléfono de Amanda? Hicimos la tabla de valores y la representamos en unos ejes.
Vamos a recordarlo:
|
Amanda ha conseguido ¡¡por fin!! convencer a sus padres de que le compren un móvil. Sus padres son muy intransigentes con este tema, de forma que la única manera de convencerlos ha sido prometiendo que sólo lo usaría para mandar SMS y no para llamar. La tarifa que han contratado es de 5 € fijos al mes con un precio de 0,18 € por cada mensaje enviado. Para controlar su gasto Amanda se ha hecho la siguiente tabla. |

|
| Imagen de Andreas_Photography en flickr bajo CC |
| x |
Número de mensajes por mes | 0 |
20 | 50 | 100 | 200 |
| y | Mensualidad que deberá pagar | 5 |
8,6 | 14 | 23 | 41 |
Que representado en unos ejes quedaba algo así:
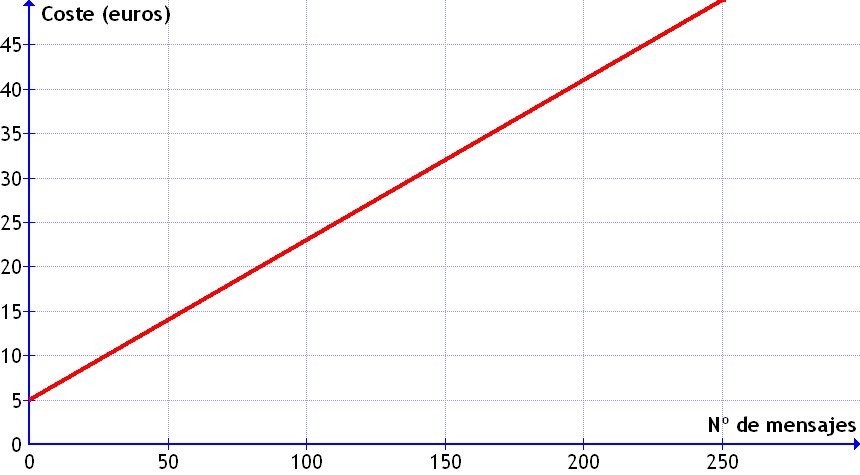
Y ¿recuerdas la forma de encontrar su ecuación matemática? Teníamos que pensar en las cuentas que hay que hacer para calcular la mensualidad de Amanda. En primer lugar hay que multiplicar el número de mensajes (la x) por el precio del mensaje (0,18 €)y después sumarle los 5 € de cuota fija (esta no depende del número de mensajes, ni siquiera de si hay alguno o no).
mensualidad = 0,18 x número de mensajes + cuota fija
Que cambiando por "x" e "y" quedaría:
y = 0,18x + 5
En este caso el coste de la mensualidad y el número de mensajes no son directamente proporcionales porque el mensaje no sale siempre al mismo coste, fíjate:
- Si Amanda manda 20 mensajes pagará una mensualidad de 8,6 €. Es decir que ese mes el mensaje le habrá salido (teniendo en cuanta el total que paga con la cuota fija) por 8,6:20 = 0,43 €
- Pero si Amanda manda 50 mensajes pagará una mensualidad de 14 €. Así que ese mes el mensaje le habrá salido (incluyendo la cuota) por 14:50 = 0,28 .
¿Ves cómo no es igual? Claro, cuantos más mensajes mande más barato le sale porque la cuota fija se reparte entre más.
Pues esto es lo que llamamos una función afín.
Actividad
Una función afín tiene las siguientes características:
- Su gráfica es una recta que no pasa por (0,0)
- Su ecuación es y = mx + b (m y b pueden ser cualquier número distinto de 0. Si b=0 tendríamos una función lineal)
- Las variables que se relacionan no son directamente proporcionales. (Si dividimos distintos valores de y entre sus x correspondientes no obtenemos el mismo número)
En el caso de las funciones afines el número que acompaña a la "x" en la ecuación, la m, sigue siendo la pendiente de la recta, y además, como en el caso anterior, indica lo que aumenta la "y" cuando la "x" aumenta una unidad. ¿No lo entiendes? no te preocupes, seguro que con el ejemplo siguiente queda aclarado:
- ¿Cuál es el valor de la pendiente en el caso de Amanda? 0,18 (porque es el número que acompaña a la "x", la m)
- ¿Tiene algún significado? es lo que vale cada mensaje sin tener en cuenta la cuota fija, es decir, es lo que aumenta la factura de Amanda (la "y") cuando ésta manda un nuevo mensaje.
¿Ahora lo entiendes? Es lo que queríamos decir. Pero vamos a insistir en la idea con el siguiente ejercicio.
Ejemplo o ejercicio resuelto
Amancio es fontanero y trabaja por su cuenta. Cobra 25 € por hora más 20 € por el desplazamiento. Para estudiar bien sus ganacias en función de las horas que emplea en la avería de una casa, Amancio se ha hecho una gráfica con su tabla de valores, su ecuación matemática y todo. ¿Podrías escribirlo todo en tu cuaderno? Cuando termines comprueba si lo has hecho bien viendo la solución.
Actividad
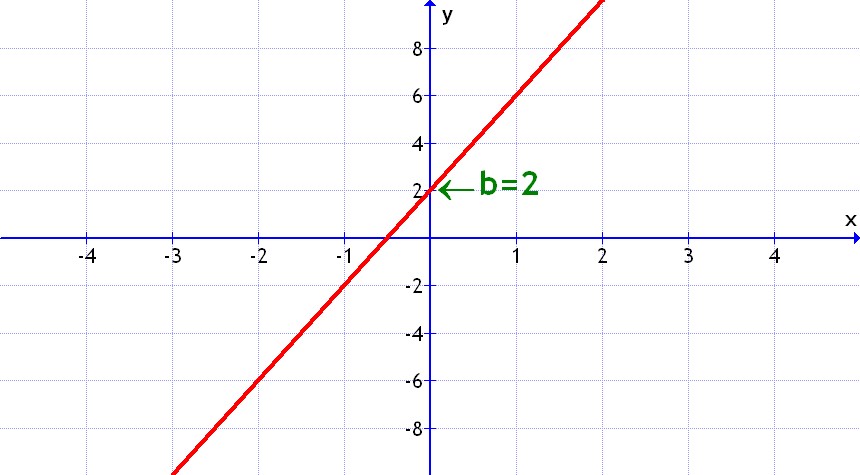
En las funciones afines y = mx + b
- El número m es la pendiente de la recta y es lo que aumenta la "y" cuando la "x" aumenta una unidad
- El número b es el punto donde la recta corta al eje de la "y" (este número se llama ordenada en el origen)