2.4 Vector aceleración

Fórmula 1

imagen bajo licencia Wikimedia Commons

Como hemos visto anteriormente, la mayoría de los movimientos que suceden en nuestro entorno no mantienen constante su velocidad. Para poder describir el movimiento que realizan hemos definido la aceleración, magnitud que nos permite cuantificar como varía la velocidad. Debemos tener en cuenta que la velocidad es una magnitud vectorial y una variación de la velocidad puede afectar a la rapidez, a la dirección o a ambas.

Cuando decimos que un coche pasa de 0 a 100 km/h todos tenemos claro que está acelerando, pero qué ocurre si circulando a 100 km/h toma una curva. La respuesta es la misma, el coche está acelerando. A diferencia de la primera situación donde lo que variaba era la rapidez del coche, es decir, el módulo de la velocidad, en esta situación lo que varía es la dirección.

Podemos hablar de una aceleración que hace que varíe la rapidez de un movimiento, a la que llamaremos aceleración tangencial. Tiene la misma dirección que la velocidad. Si tiene su mismo sentido el móvil aumentará su velocidad (acelerará) y si tiene sentido contrario el móvil disminuirá su velocidad (frenará)

Por otro lado llamamos aceleración normal la que hace que varíe la dirección del movimiento. Esta aceleración es perpendicular al vector velocidad.

 

 

Importante

Podemos hablar de aceleración en un movimiento si cambia la rapidez, si cambia la dirección o si lo hacen ambas.
En el S.I. de unidades la  aceleración  se expresa en m/s2

AV - Pregunta Verdadero-Falso

Indica si las afirmaciones siguientes son ciertas o falsas.

Pregunta 1

Una moto toma una curva cerrada a 50 km/h. Por tanto, no lleva aceleración.

Sugerencia

Pregunta 2

En una contrarreloj, un ciclista rueda a 55 km/h por una carretera llana y recta. En esas condiciones su aceleración es cero.

Sugerencia

Pregunta 3

Un avión de la patrulla acrobática realiza un looping vertical. Mientras lo hace, la aceleración es nula.

Sugerencia

AV - Pregunta de Elección Múltiple

Pregunta

La aceleración de una moto es de 6 m/s2. Partiendo del reposo, al cabo de 5 s su velocidad es de:

Respuestas

25 m/s

30 m/s

-15 m/s

Retroalimentación

Ejemplo o ejercicio resuelto

Comparad la aceleración tangencial de dos vehículos que acceden a la autopista: El vehículo A, parado inicialmente en el peaje, alcanza una rapidez de 108 km/h al cabo de 10 s; y el vehículo B, que se ha incorporado desde la vía de servicio a 36 km/ h, tarda 8 s en alcanzar los 108 km/h.

Al tratarse de un movimiento en una dimensión, la carretera, vamos a prescindir del tratamiento vectorial.

Vehículo A

v0= 0 m/s

vf =108 km/h = 30 m/s

Δt = 10 s

a= ?

 

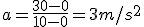
Vehículo B

v0= 36 km/h = 10 m/s

vf= 108 km/h = 30 m/s

Δt= 8 s

a = ?

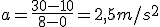
Ejemplo o ejercicio resuelto

Dos trenes circulan en sentidos contrarios por la misma vía y, para evitar el choque, frenan hasta pararse. Sabiendo que el tren que viaja a 12 m/s tarda 8 s en detenerse, y que el que viaja a 20 m/s se para en 10 s, calculad la aceleración tangelcial de cada uno, e interpretad el signo obtenido.

 

Tomaremos como sentido positivo el del movimiento del tren A

Tren A

V0 = 12 m/s

vf = 0 m/s

Δt = 8

→

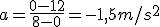
Este tren reduce su velocidad a razón de 1,5 m/s cada segundo, ya que la aceleración va sentido contrario a la velocidad.

Tren B

V0 = -20 m/s (El signo - se debe a que este tren se mueve en sentido contrario al tren A)

vf = 0 m/s

Δt =10 s

→

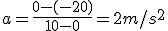
Este tren reduce su velocidad a razaón de 2 m/s cada segundo, ya que la aceleración va sentido contrario a la velocidad, y se detendrá antes que el tren A

AV - Pregunta Verdadero-Falso

Si un móvil parte de un punto situado a 15 m a la izquierda del origen y se mueve con una rapidez de 15 m/s y una aceleración de - 1 m/s2 el movimiento será:

Pregunta 1

a) acelerado

Pregunta 2

b) decelerado

Importante

El signo de la aceleración, por sí solo, no nos da información sobre si el móvil disminuye o aumenta el valor absoluto de su rapidez, es decir sobre si «frena» o «acelera».
A modo de conclusión y de cara al estudio que vamos a hacer en los siguiente temas, los movimientos se pueden clasificar según el valor de la aceleración y de la velocidad.
  • Movimientos rectilíneos y uniformes: son aquellos que no poseen aceleración
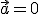
  • Mivimientos rectillineos uniformemente acelerados: son aquellos donde la aceleración tangencial es constante
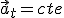
  • Movimientos circulares uniformes: son aquellos donde la aceleración normal es constante
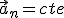
  • Movimientos circulares uniformemente acelerados: son aquellos en que la aceleración tangencial yla normal son constanes 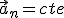y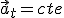
Tipo de movimiento
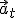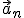M.R.U cte 0 0
M.R.U.A ≠ cte cte 0
M.C.U ≠ cte 0 cte
M.C.U.A
 ≠ cte ≠ cte ≠ cte