Resumen

Importante

Ángulo plano

Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. El ángulo es positivo si se desplaza en sentido contrario al movimiento de las agujas del reloj y negativo en caso contrario.

ángulo

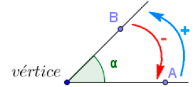
Para medir ángulos empleamos grados o radianes. Un radián es el ángulo cuyo recorrido es igual al radio con que ha sido trazado

cambio de unidades de ángulos

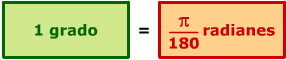
Importante

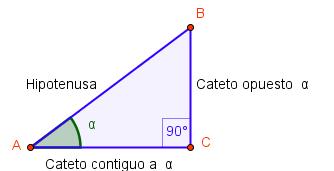
Para un ángulo agudo α se define el seno de α, se escribe sen α, como el cociente entre el cateto opuesto a α y la hipotenusa del triángulo rectángulo ABC construido sobre α.

sen α =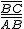

Para un ángulo agudo α se define el coseno de α, se escribe cos α, como el cociente entre el cateto contiguo a α y la hipotenusa del triángulo rectángulo ABC construido sobre α.

cos α =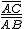

De manera similar, se define la tangente de α, se escribe tg α, como el cociente entre el cateto opuesto a α y el cateto contiguo del triángulo rectángulo ABC construido sobre α.

tg α =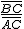

Como hemos podido comprobar, el valor del seno, coseno y tangente de α no depende del tamaño del triángulo ABC.

Importante

Relaciones fundamentales de la trigonometría.

1) sen² α + cos² α = 1

2) tg α =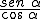

Importante

Razones trigonométricas de la suma de dos ángulos α y β

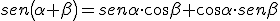
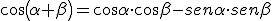
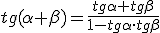
Veamos ahora las fórmulas análogas a las anteriores para la diferencia de dos ángulos.

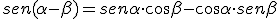
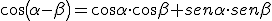
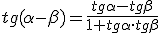
Importante

Las razones trigonométricas del ángulo doble.

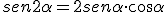
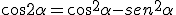
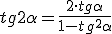
Las razones trigonométricas del ángulo mitad:

$sen(\frac{\alpha}{2})=\pm\sqrt { \frac { 1-cos \alpha }{ 2 } }$

$cos(\frac{\alpha}{2})=\pm\sqrt { \frac { 1+cos \alpha }{ 2 } }$

$tg(\frac{\alpha}{2})=\pm\sqrt { \frac { 1-cos \alpha }{ 1+cos \alpha} }$

Importante

Un número complejo z=a+bi puede expresarse en función de su módulo , que designaremos por r, y del ángulo que forma el vector (a,b) con el semieje positivo del plano complejo, de la forma polar:

Donde:

r=módulo de z=

se conoce también como el argumento de z (arg(z)) y se halla con la calculadora científica de la siguiente forma .Siendo .