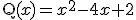1.2. Operaciones con polinomios

Una vez que ya conoces el valor numérico de un polinomio, veremos las operaciones con polinomios. Al igual que operas con números naturales, enteros o reales, podemos trabajar con polinomios, sumando, restado, multiplicando y dividiendo estos. 

Importante

SUMA Y RESTA DE POLINOMIOS

Para sumar o restar polinomios, tan solo debemos operar con los monomios que tengan la misma parte literal, recordando que la parte literal es la variable con su exponente.

Si pretendemos calcular la suma de los polinomios P(x) = x2-4x+4 y Q(x) = 3x2+5x-3, simplemente sumamos los coeficientes de las partes literales P(x)+Q(x) = (1+3)x2+(-4+5)x+(4-3) = 4x2+x+1.

También podemos colocar en vertical los sumandos y realizar la operación

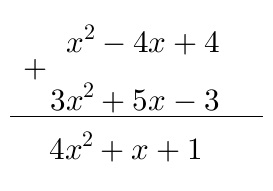Para restar polinomios, actuamos de forma análoga, podemos restar los coeficientes de las partes literales o simplemente colocarlos de forma vertical y operar.

Si M(x) = x3-3x+5 y N(x) = 2x3-x2+4x-2 , el resultado de la resta es M(x)-N(x) = (1-2)x3+(0-(-1))x2+(-3-4)x+(5-(-2))=-x3+x2-7x+7. También podemos operar de forma vertical

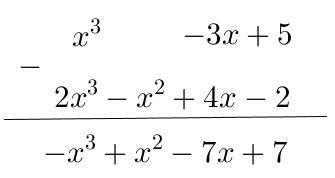Actividad de rellenar huecos

Si B(x) = 3x3-3x2+4x-1 y A(x) = x3-6x2+4. Calcula C(x)=B(x) + A(x) y D(x) = B(x)-A(x). Rellena los siguientes huecos.

C(x) = x3- x2+ x+

D(x) = x3+ x2+ x-

Enable JavaScript

Actividad

MULTIPLICACIÓN DE POLINOMIOS

  • Al multiplicar un monomio por un polinomio, tan solo debemos aplicar la propiedad distributiva.
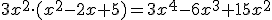3x^2\cdot(x^2-2x+5) = 3x^4-6x^3+15x^2

 

  • Si queremos multiplicar dos polinomios, aplicaremos reiteradamente la propiedad distribuitiva.
(3x^2+2x+1)\cdot(x^2-3)=3x^2\cdot(x^2-3)+2x\cdot(x^2-3)+1\cdot(x^2-3)= 3x^4-9x^2+2x^3-6x+x^2-3=3x^4+2x^3-8x^2-6x-3

Caso de estudio

Máquina diferencial de Babbage para cálculos con polinomios
Imagen en Flickr de Ric e Ette bajo CC

Calcula el producto de los polinomios

\rm{P}(x) = x^3-2x^2+x+1 y \rm{Q}(x) = x^2-4x+2

Pregunta de Elección Múltiple

Pregunta

El producto de los polinomios \rm{P}(x) = x^3-x^2+x-1 y \rm{Q}(x) = 2x^2-3 es:

Respuestas

2x5+2x4-x3-3x+3

2x5-2x4-x3+x2-3x+3

2x5-2x4-x3+x2-3x-3

2x5+2x4-x3+x2-3x+3

Retroalimentación

Reflexión

Dados los polinomios A(x) = x3-3, B(x) =x2-3x+4 y C(x) = x+4, calcula A·B, A·C y B·C

Actividad

DIVISIÓN DE POLINOMIOS

    • División de monomios.
      Dividimos  los coeficientes y las partes literales. Ejemplo 3x5:2x2=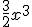 \frac{3}{2}x^3



    • División de un polinomio entre un monomio.
      Dividimos cada término del polinomio entre el monomio. Ejemplo (3x4-2x3+3x):3x =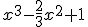



  • División de un polinomio  entre un polinomio.
  1. Ordenamos los polinomios según las potencias y de mayor a menor.
  2. Se dividen los primeros términos del dividendo y del divisor.
  3. El resultado obtenido se multiplica por el divisor y se resta al dividendo.
  4. Seguimos este procedimiento hasta que el resto sea de un grado menor que el divisor. Ejemplo:(3x4-2x3+4x2+2x-2):(x2-2x-1)

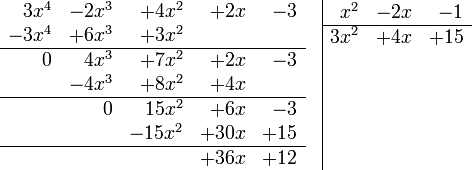Imagen en Wikipedia bajo Dominio Público

Caso de estudio

Realiza la división de los polinomios x3+3x2-3x-6 y x2-2x+1

Actividad de rellenar huecos

Calcula la división de los polinomios 3x3-5x+1 y x+3                           

Montaña rusa
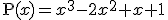Imagen en Flickr de hounddiggity bajo CC
(3x3-5x+1):(x+3) = x2- x+     Resto:

Enable JavaScript