2.2 Ondas estacionarias
Llegados a este punto, se debe hacer una distinción entre ondas viajeras y ondas estacionarias.
Se considera una onda viajera a aquella que a lo largo del tiempo su perfil va variando. Un ejemplo sería las olas.
Por el contrario, en una onda estacionaria ese perfil no se mueve. Y el fenómeno suele aparecer en medios reducidos, como en una cuerda de un violín o guitarra. En esos medios se puede lograr una oscilación que no avanza ni retrocede.
Los vídeos siguientes te pueden aclarar mejor el asunto de las ondas estacionarias, en uno verás cómo la arena se coloca en unas posiciones determinadas y no cambian de lugar a pesar del movimiento y en otro podrás observar cómo un puente adquiere un movimiento hasta que se fractura debido a una resonancia.
| Vídeo de Simon Lespérance alojado en Youtube | Vídeo de Universidad de Alicante alojado en Youtube |
Las ondas estacionarias no son ondas de propagación sino los distintos modos de vibración de una cuerda, una membrana, etc. Una onda estacionaria se puede considerar como la interferencia de dos ondas de la misma amplitud y longitud de onda: una que se propaga de izquierda a derecha y otra que se propaga de derecha a izquierda.
| Grabación de Simulación de Jesús Peñas bajo licencia Creative Commons |
Estas ondas se producen entre ondas coherentes, recuerda que esta condición significa que la diferencia de fase entre ambas ondas es constante, lo que permite que la interferencia se estable y podamos verla. La interferencia tiene lugar cuando una onda se refleja en la misma dirección en la que se propaga, pero en sentido contrario. Las dos ondas que se superponen. Este fenómeno suele ocurrir cuando una onda directa se combina con su reflejada dando lugar a una onda resultante estacionada.
La onda presenta unos puntos fijos que no vibran que se conocen por nodos y el resto de puntos que vibran como si se tratase de un conjunto de osciladores armónicos, cada uno con su amplitud determinada, por lo que el perfil de la onda no se desplaza, está quieto.
Importante
La ecuación que representa a una onda estacionaria puede conseguirse sin más que sumar algebraicamente las ecuaciones de las ondas que se afectan. La única diferencia entre las ondas que interfieren es su sentido de propagación, de modo que las ecuaciones a sumar serán:
![]()
Sumando y teniendo en cuenta las relaciones trigonométricas, dependiendo de las condiciones en las que se produzca la reflexión, la resultante puede ser:
![]() o bien
o bien ![]()
Analizando la expresión anterior podrás distinguir, en cualquiera de las soluciones, dos partes bien diferenciadas. Una que depende del tiempo y otra que varía con la posición. La primera de ellas muestra que en un determinado lugar la partícula situada allí o el punto oscila con un movimiento armónico simple de la misma frecuencia que las perturbaciones que originan la onda. Lo mismo ocurre en todos los puntos del medio en el que la onda estacionaria está confinada.
La otra parte de la ecuación representa la dependencia espacial. El término viene a expresar la amplitud del movimiento armónico simple antes citado para cada punto a una distancia determinada del origen inicial de la onda. Lo particularmente curioso e interesante es la amplitud del movimiento. La elongación máxima del movimiento para cada punto es diferente, no siendo un valor constante, sino que depende sinusoidalmente de la posición y, por tanto, cada punto del medio oscila con su propia amplitud.
Si te fijas en la primera solución, existen algunos puntos que tienen amplitud nula. En tales puntos se cumple que ![]() . Dichos puntos permanecen en reposo de forma continua y se encuentran localizados para
. Dichos puntos permanecen en reposo de forma continua y se encuentran localizados para ![]() . Tales posiciones son los nodos.
. Tales posiciones son los nodos.
En cambio, los puntos en los que se verifique que ![]() oscilarán con amplitud máxima e igual a dos veces a la amplitud de la onda original. Tales puntos serán los vientres o antinodos de la onda estacionaria. Un punto será un vientre si, para un valor de
oscilarán con amplitud máxima e igual a dos veces a la amplitud de la onda original. Tales puntos serán los vientres o antinodos de la onda estacionaria. Un punto será un vientre si, para un valor de ![]() , se verifica
, se verifica![]()
Vamos a estudiar ahora una cuerda de longitud L fija en los extremos. La cuerda tiene un conjunto de modos normales de vibración, cada uno con una frecuencia característica.
Los extremos de la cuerda deben de ser nodos ya que estos puntos se encuentran fijos. El primer modo de vibración será aquel en el que la longitud de la cuerda sea igual a media longitud de onda L= 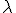 /2. Para el segundo modo de vibración, la longitud de la cuerda será igual a una longitud de onda, L=
/2. Para el segundo modo de vibración, la longitud de la cuerda será igual a una longitud de onda, L= 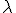 . Para el tercer modo, L=3
. Para el tercer modo, L=3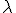 /2, y así sucesivamente.
/2, y así sucesivamente.
| Grabación de Simulación de Jesús Peñas bajo licencia Creative Commons |
El caso de la vibración de una cuerda sujeta por los dos extremos es el ejemplo típico de las cuerdas de los instrumentos musicales. El hecho de que los dos extremos estén fijos, y por tanto necesariamente de amplitud nula en todo momento, impone una fuerte restricción sobre las ondas que se pueden propagar en el seno de tales cuerdas.
Las frecuencias permitidas reciben el nombre de frecuencias de resonancia. La más baja de todas, se denomina fundamental o primer armónico.
En la simulación se ve la existencia de nodos y antinodos (o vientres), para cada armónico, es decir puntos de amplitud nula y máxima respectivamente. Como se observa en la simulación, la condición de resonancia para el armónico de orden n es:
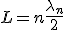
donde n = 1, 2, 3...
Ejemplo o ejercicio resuelto
Para saber más
Los modos de vibración de una cuerda, por ejemplo la de un instrumento musical, dependen de la longitud de la cuerda, de la tensión a la que está sometida y de la densidad lineal que es una característica de la cuerda que representa la masa por unidad de longitud.
Las frecuencias de la vibración las podemos deducir como:

Según esto la frecuencia fundamental es:

La velocidad de propagación de la onda en una cuerda es:
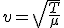
donde 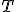 es la tensión de la cuerda y
es la tensión de la cuerda y 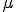 la densidad lineal de la cuerda (masa por unidad de longitud).
la densidad lineal de la cuerda (masa por unidad de longitud).
Por lo tanto las frecuencias de los armónicos las podemos expresar como:
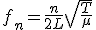
donde n vale 1 para el primer armónico, 2 para el segundo armónico y así sucesivamente.
Ejemplo o ejercicio resuelto
Caso práctico
|
|
Imagina esta vista. Se parecen mucho a una onda estacionaria. Ahora evade tu mente y piensa que está formada por dos ondas armónicas se propagan por el mismo medio en sentidos opuestos.
Si las ondas tienen una amplitud de 12 cm, una frecuencia de 1,6 Hz y una velocidad de propagación de 1,6 m/s. ¿Cuál es la ecuación de la onda estacionaria que producirá su interferencia? ¿Con qué amplitud vibrarán los puntos x = 0,3 cm, x = 0,5 cm y x = 1,5 cm? ¿Qué distancia habrá entre dos nodos consecutivos?
