2.1 Interferencia entre dos ondas
Las ondas que interfieren pueden proceder de dos fuentes distintas. Nosotros vamos a estudiar un caso muy importante que es cuando las ondas que interfieren proceden de dos fuentes síncronas. En este caso se trata de ondas coherentes, es decir, con longitud de onda, frecuencia y amplitud iguales, y sus fases o bien son iguales, o bien presentan una cierta discrepancia que permanece constante. En este caso la interferencia es detectable y presenta un patrón permanente en el que hay mucha diferencia entre la intensidad de los máximos y los mínimos.
Si la diferencia de distancias recorridas desde la fuente es un número entero de longitudes de onda, las ondas están en fase y la interferencia será constructiva. En los puntos que se cumple la condición se produce un máximo. Es decir, la condición de máximo es: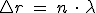 
| Grabación de Simulación de Jesús Peñas bajo licencia Creative Commons |
Si la diferencia de distancias recorridas desde la fuente es un número impar de semilongitudes de onda, las ondas están desfasadas en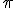 
y la interferencia será destructiva. En los puntos que se cumple la condición se produce un mínimo. Es decir, la condición de mínimo es: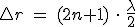 
| Grabación de Simulación de Jesús Peñas bajo licencia Creative Commons |
AV - Reflexión
 |
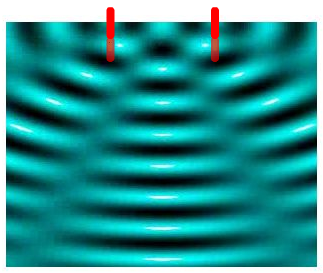| Imagen de jepeca bajo licencia Creative Commons |
En la superficie de un pequeño estanque haces oscilar dos punzones separados una distancia de 2 cm. Los punzones generan ondas coherentes con una frecuencia de 12 Hz. La velocidad de propagación de las ondas es de 3 cm/s. ¿Cuál es el resultado de la superposición en un punto que dista 15 cm de un punzón y 13,5 cm del otro?
Un caso muy interesante es el de la superposición de dos ondas armónicas de la misma amplitud y frecuencia.
| Grabación de Simulación de Jesús Peñas bajo licencia Creative Commons |
El resultado de la superposición es otra onda armónica de la misma frecuencia y velocidad de propagación que las ondas originales y cuya amplitud es:
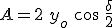, donde 
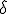es el desfase.
La amplitud de la onda resultante depende de la amplitud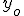
de las ondas que se superponen y del desfase 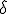entre ellas.
Si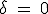 
, las ondas están en fase y la amplitud resultante es 
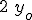. Si 
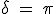, la amplitud resultante es nula. En el primer caso se habla de interferencia constructiva y en el segundo de interferencia destructiva, pudiendo darse todas las situaciones intermedias según la diferencia de fase.
Ejemplo o ejercicio resuelto
Dos ondas armónicas longitudinales que se propagan por un mismo medio y en la misma dirección, vienen dadas por las ecuaciones (en unidades del S.I.):
e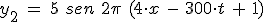 
¿Cuál es la amplitud, la frecuencia, la longitud de onda y la velocidad de propagación de la onda resultante?
AV - Reflexión
Dos ondas armónicas vienen dadas por:
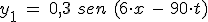e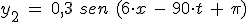 
Si se superponen, ¿cuál es la velocidad de propagación de la onda resultante?
Cuando las frecuencias de las ondas que se superponen son diferentes la interferencia produce una onda más compleja. Puedes comprobarlo en la siguiente simulación en la que se superponen dos ondas de la misma amplitud con las frecuencias seleccionadas.
| Grabación de Simulación de Jesús Peñas bajo licencia Creative Commons |