2.3. Producto de matrices
Ejemplo o ejercicio resuelto
 |
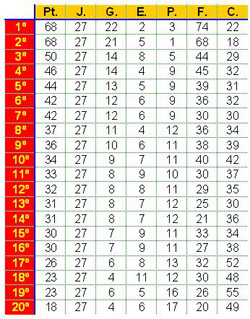Retomamos la tabla de clasificación de los equipos en un determinado momento de la liga, sin los nombres de los equipos, en la que puedes ver que aparecen los puntos del equipo, los partidos jugados hasta ese momento, entre ellos cuántos se han ganado, empatado o perdido y, por último, los goles a favor y en contra.
Si solamente conociésemos los partidos ganado, perdidos y empatados, podríamos conocer el número de partido jugados. Además, podríamos conocer el número de puntos que tiene el equipo ya que conocemos que obtiene 3 puntos por cada partido ganado, un punto por cada partido empatado y 0 puntos por cada partido perdido.
De la tabla anterior podemos obtener la matriz que contiene el número de partidos ganados, el número de partidos empatados y el número de partidos perdidos de cada equipo:
Además, la matriz que nos indica el número de puntos que se le da a un equipo por cada partido ganado, empatado o perdido es la siguiente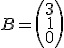 
Si a partir de estas dos matrices queremos calcular el número de puntos que tiene cada equipo, deberíamos multiplicar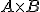 
. ¿Sabes cómo hacerlo?... En la solución te lo explicamos.
Si ahora consideramos la matriz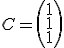 
Si multiplicamos 
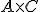¿sabes qué obtendríamos?
Y si ahora consideramos la matriz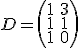 
Si multiplicamos 
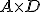¿Sabrías hacerlo? ¿Sabes qué obtendríamos?
No te preocupes, que ahora te desvelamos todos estos secretos
Fijémonos en el producto 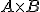. Lo que hemos hecho es multiplicar cada elemento de la primera fila de la matriz 
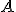por el elemento correspondiente de la primera columna de la matriz 
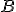. Para poder hacer lo anterior, el número de elementos que la matriz 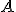tiene en esa fila (3 elementos en nuestro caso) es el mismo número de elementos que tiene 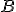en su columna, en nuestro caso 3 también.
En el ejemplo anterior, la matriz 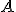tiene 20 filas y 3 columnas y la matriz 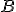tiene 3 filas y 1 columna. Cuando realizamos el producto 
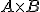nos resulta una matriz que tiene 20 filas y 1 columna. En resumen.
| |
|
|
 |
 |
 |
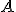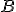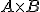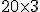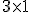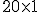Observa qué ocurre en los casos de los productos 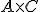y 
.
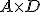Piensa si se podría hacer el producto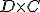 
.
Importante
Si tenemos dos matrices 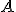de orden 
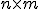y 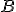de orden 
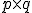, el producto 
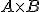es otra matriz cuyos elementos se obtienen multiplicando de forma ordenada cada fila de la matriz 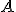por todas las columnas de la matriz 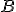. Así, el elemento que ocupa la posición 3,7 en la matriz resultante es el resultado de multiplicar la fila 3 de la matriz 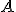por la columna 7 de la matriz 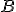, es decir, cada elemento de la fila 3 de la matriz 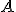se multiplica por el elemento correspondiente de la columna 7 de la matriz 
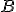y se suman los resultados.
Por tanto, el número de elementos que tiene la matriz 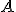en cada fila (número de columnas de 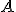) tiene que coincidir con el número de elementos que tenga la matriz 
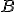en cada columna (número de filas de 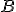). En nuestro caso, para que se puedan multiplicar A y B debe cumplirse que 
.
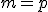Dicen que una imagen vale más que mil palabras. Te proponemos el siguiente ejercicio resuelto para que compruebes si has captado como se realiza esta operación con matrices...
Ejemplo o ejercicio resuelto
Si tenemos dos matrices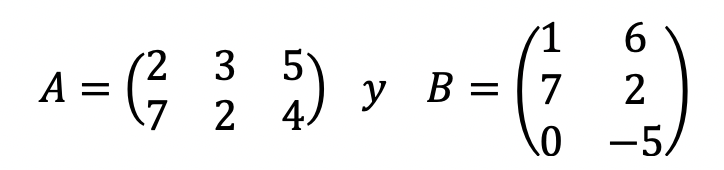 
Piensa qué producto podemos hacer AxB ó BxA. Cuando lo sepas, calcula el que se pueda hacer o los que se puedan hacer.
Recuerda que en un producto de matrices, el número de columnas de la primera debe ser igual que el número de filas de la segunda.
Entra en el siguiente enlace y responde a las preguntas del test que aparece para saber lo que has aprendido hasta ahora.
Entra en el siguiente enlace y realiza productos de matrices para comprobar tus destrezas. Cada vez que pulses el botón "Autogenerar" aparecerán dos matrices nuevas. Cuando hayas realizado el producto, pulsa sobre el botón "Comprobar" para comprobar el resultado.
AV - Reflexión
Bueno, ahora ya conoces bastante sobre las matrices y conoces cómo deben ser dos matrices para poder multiplicarlas. Echa un vistazo a esta aplicación de GeoGebra para saber cómo multiplicar matrices.
Importante
Igual que si multiplicas cualquier número por 1 obtienes el mismo número, hay una matriz que tiene el mismo efecto. La matriz identidad I, que viste en el punto 1.2, cumple que si la multiplicas por cualquier otra matriz, al final nos queda esa segunda matriz.
Recuerda que la matriz identidad está formada por 1 en la diagonal y 0 en el resto de elementos. Por ejemplo, la matriz identidad de orden 2 es:
Compruébalo escribiendo cualquier matriz y multiplicándola por la matriz identidad del orden conveniente para poder hacer el producto. Verás que obtienes la matriz del principio.