1.2. Tipos de matrices
 |
Quizás recuerdes que el curso pasado trabajamos con los vectores; en particular con los de dos elementos 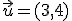 . Si te fijas podemos considerar que ese vector (3 4) es un caso particular de matriz en la que sólo hay una fila. En este apartado vamos a ver distintos tipos de matrices que por alguna característica particular reciben un nombre específico.
. Si te fijas podemos considerar que ese vector (3 4) es un caso particular de matriz en la que sólo hay una fila. En este apartado vamos a ver distintos tipos de matrices que por alguna característica particular reciben un nombre específico.
En la siguiente presentación puedes ver las definiciones, ilustradas con ejemplos, de diversos tipos de matrices. Si pulsas en la flecha de avance de la parte inferior izquierda podrás ver los tipos que hay.
Para comprobar si has entendido todas las definiciones puedes practicar en los siguientes enlaces:
- En Crucigrama de matrices con sólo pulsar en cada número te aparecerá una pregunta y la ventana para que escribas la solución. Sólo hay una pregunta cuya solución no hemos visto aún. Corresponde a la pregunta 7 y cuya respuesta es SARRUS.
- En Test de matrices repasarás lo que hemos visto hasta el momento a través de una serie de preguntas tipo test. Hay dos preguntas, la 7 y la 10, que corresponden a elementos que veremos en el apartado 2.4.
AV - Pregunta Verdadero-Falso
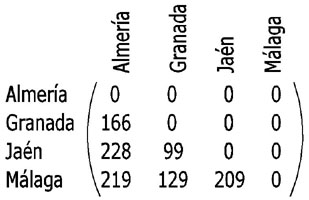 |
En muchos mapas de carreteras aparece la información sobre las distancias entre las capitales de provincias o de países. A partir de esa información podemos construir una matriz de distancias como la siguiente, en la que, para no repetir datos, sólo se escribe la distancia de una ciudad a otra, no de la otra a la una, nos explicamos, si escribimos la distancia de Barcelona a Madrid, no se escribe también la de Madrid a Barcelona, sino que se escribe 0.
En la imagen adjunta tienes la matriz de distancias que hemos construido con los kilómetros que hay entre las capitales de Andalucía Oriental. A partir de ellas responde si son ciertas o falsas las siguientes afirmaciones.
Retroalimentación
Verdadero
Sí porque tiene el mismo número de filas que de columnas.
Retroalimentación
Verdadero
Es cierto porque todos los elementos aii son nulos.
Retroalimentación
Falso
No, más bien es triangular inferior.
Retroalimentación
Verdadero
Es cierto ya que esos términos son precisamente los que están por encima de la diagonal principal.
Retroalimentación
Falso
No, quien vale 129 es el término a42.