6. Derivadas. Aplicaciones
Importante
 |
Pensando en la prueba...
El cálculo de derivadas y su aplicación a la representación de funciones, son actividades que suelen aparecer con mucha frecuencia. Si bien es cierto, que solo aparecen en problemas propios de la parte de análisis, a diferencia de lo que ocurriría, por ejemplo, con las ecuaciones y sistemas, que se pueden utilizar como herramientas para resolver otras actividades.
|
Imagen de elaboración propia |
Variación media y variación instantánea. Interpretación geométrica
Dada una función  se llama variación media de
se llama variación media de 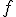 en un intervalo
en un intervalo  al cociente:
al cociente:
Al ser la variación media un cociente de variaciones las unidades en que se expresa son también cociente de unidades.
Geométricamente, la tasa de variación media de la función 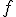 en el
intervalo
en el
intervalo  es la pendiente de la recta secante a la gráfica de
es la pendiente de la recta secante a la gráfica de 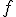 que pasa por los puntos
que pasa por los puntos  y
y  .
.
La tasa de variación instantánea de una función 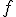 en el punto
en el punto  es:
es:
Derivada en un punto. Interpretación geométrica
Si tenemos una función  llamamos derivada de la función en un punto
llamamos derivada de la función en un punto  a la tasa de variación instantánea de la función
a la tasa de variación instantánea de la función 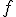 en el punto
en el punto  y se denota por
y se denota por 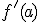 . Así, según la definición tenemos que:
. Así, según la definición tenemos que:
Recuerda que para que exista este límite, deben existir los límites laterales y coincidir. Así, de la misma forma, podemos definir las derivadas laterales como:
- Derivada por la derecha:
- Derivada por la izquierda:
En el caso de que ambos límites coincidan diremos que la función 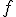 es derivable en el punto
es derivable en el punto  .
.
Geométricamente, la derivada de una función en un punto es la pendiente de la recta tangente a la gráfica de la función en dicho punto, ya que las rectas secantes en el entorno de un punto tienden a confundirse con la recta tangente en el punto a medida que los incrementos se hacen más pequeños.
Función derivada. Reglas de derivación. Derivadas sucesivas
Dado que la derivada es un concepto local podría definirse la función derivada en aquellos puntos en que la función primera o primitiva es derivable.
Si tenemos una función  denominamos función derivada de
denominamos función derivada de 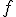 respecto a la variable
respecto a la variable  a una nueva función que para cada valor
a una nueva función que para cada valor  nos proporciona la derivada de la función en el punto
nos proporciona la derivada de la función en el punto  . A la función derivada de
. A la función derivada de  la denotaremos
la denotaremos 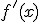 , aunque también la puedes ver representada como
, aunque también la puedes ver representada como ![]() . De esta forma, tenemos que:
. De esta forma, tenemos que:
Recuerda que con esta definición, la función derivada nos proporciona, para cada punto  , la pendiente de la recta tangente a la función en punto
, la pendiente de la recta tangente a la función en punto  .
.
Todos los resultados que aparecen en la siguiente tabla son fruto de aplicar la definición de derivada de una función. Te recomendamos que para no tener que recurrir una y otra vez a esta definición, te aprendas el siguiente cuadro. No te asustes, es más sencillo de lo que parece, el secreto está en la práctica.
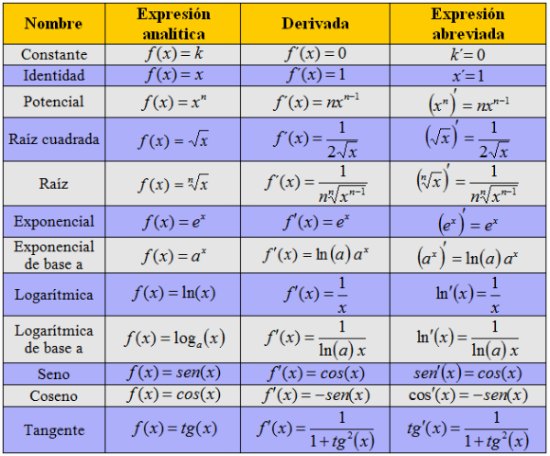
Además, tampoco es frecuente que nos pregunten por derivadas de funciones elementales, sino por la composición, suma, producto... de varias. Por ello, también debes tener en cuenta las siguientes reglas:
| Suma | 
|
La derivada de la suma de funciones es la suma de las derivadas de estas funciones |
| Resta | 
|
La derivada de la diferencia de funciones es la diferencia de las derivadas de estas funciones |
| Producto |
 |
La derivada del producto de dos funciones es igual a la derivada de la primera por la segunda sin derivar más la segunda derivada por la primera sin derivar. |
| Cociente |
 |
La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador sin derivar menos la derivada del denominador por el numerador sin derivar, y todo ello dividido por el denominador al cuadrado |
| Producto por un número | 
|
La derivada del producto de un número real por la función es igual al número real por la derivada de la función |
| Composición |

|
|
A la derivada de una función también se la denomina derivada primera. Si volvemos a derivar la derivada primera de una función, obtenemos la llamada derivada segunda; la derivada de la derivada segunda se denomina derivada tercera; y así sucesivamente. Estas son las llamadas derivadas sucesivas de una función:
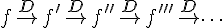
Aplicación de la derivada a la representación de funciones
Conceptos relacionados con el estudio de f
- Dominio, los valores para los cuales está definida la función.
- Simetría. Existen dos tipos de simetría:
- Una función es simétrica respecto al eje de ordenadas (OY), si para todo valor,
 , de su dominio se cumple que:
, de su dominio se cumple que: 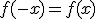 . En este caso decimos que la función es par.
. En este caso decimos que la función es par.
- Una función es simétrica respecto al origen de coordenadas, si para todo valor,
 , de su dominio se cumple que:
, de su dominio se cumple que:  . En este caso decimos que la función es impar.
. En este caso decimos que la función es impar.
- Puntos de corte con los ejes.
- El punto de corte de la función con el eje vertical, eje de ordenadas o eje OY, es aquel en el que la variable se hace cero. Por lo tanto, basta anular la variable en la función para obtener la ordenada del punto de corte. Es decir, en la función
 será un punto de la forma
será un punto de la forma 
- Por su parte, el corte de la gráfica de la función con el eje de abscisas, eje horizontal o eje OX, corresponderá a un valor de
 que anule la función. Es decir, si se verifica que
que anule la función. Es decir, si se verifica que  , entonces el punto de corte con el eje horizontal será
, entonces el punto de corte con el eje horizontal será  .
.
- Asíntotas. Dada una función
 cuya gráfica es la curva
cuya gráfica es la curva  se dice que la recta
se dice que la recta  es una asíntota de
es una asíntota de  si la curva
si la curva  se acerca a
se acerca a  indefinidamente sin llegar a coincidir con la propia
indefinidamente sin llegar a coincidir con la propia  . Tenemos 3 tipos de asíntotas: verticales, horizontales y oblicuas.
. Tenemos 3 tipos de asíntotas: verticales, horizontales y oblicuas.
Conceptos relacionados con el estudio de f'
- Monotonía. Es el comportamiento de una función respecto a su crecimiento o decrecimiento. Sea
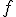 una función derivable en un intervalo
una función derivable en un intervalo  , entonces:
, entonces:
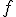 es creciente en el intervalo
es creciente en el intervalo  si
si  en todo el intervalo
en todo el intervalo  .
.
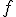 es decreciente en el intervalo
es decreciente en el intervalo  si
si  en todo el intervalo
en todo el intervalo  .
.
- Extremos. Una función
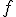 , continua y derivable en un intervalo
, continua y derivable en un intervalo  , alcanza sus máximos y mínimos relativos en los puntos del intervalo
, alcanza sus máximos y mínimos relativos en los puntos del intervalo  en los que
en los que  . Además, si estudiamos la segunda derivada,tendremos un
. Además, si estudiamos la segunda derivada,tendremos un
- Máximo relativo si
 y
y 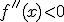 .
. - Mínimo relativo si
 y
y  .
.
Conceptos relacionados con el estudio de f''
- Curvatura. En una función dos veces derivable, podemos estudiar la curvatura de la siguiente forma:
- Convexa(U) en los intervalos donde
 .
.
- Cóncava(∩) en los intervalos en los que
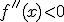 .
.
- Puntos de inflexión son los puntos donde cambia la curvatura. Por tanto se cumple que
 . Para que efectivamente sean puntos de inflexión debe cumplirse en ellos, además, que
. Para que efectivamente sean puntos de inflexión debe cumplirse en ellos, además, que  .
.
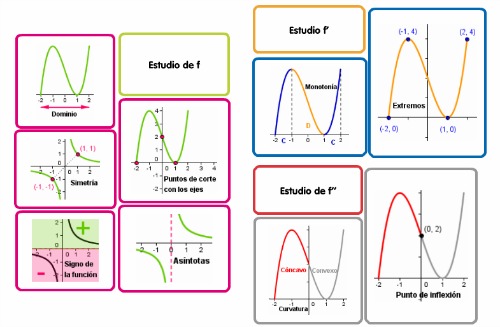 |
|
| Imagen de elaboración propia. Haz clic para ampliar |
Caso de estudio
 |
Curso 2009/2010
Dada la función ![]() determine las regiones de crecimiento y decrecimiento de la función.
determine las regiones de crecimiento y decrecimiento de la función.
Caso de estudio

|
Curso 2009/2010
Calcule la derivada de la función: ![]()
Caso de estudio
 |
Curso 2010/2011
Calcule las derivadas de las funciones: ![]() y
y ![]() .
.
Caso de estudio
 |
Curso 2010/2011
(Continuación)
Estudie si la siguiente función es derivable en  :
:

