3. Álgebra
Importante
 |
Pensando en la prueba...
El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades, por lo que te podrás hacer una idea de la importancia que tiene. En la prueba este hecho no se pasa por alto, nos encontramos con ejercicios de inecuaciones, sistemas y ecuaciones explícitamente, y con otros en los que se tienen que utilizar estas herramientas, ya que es necesario calcular parámetros o constantes a partir de unas condiciones.
Expresiones algebraicas
Una expresión algebraica es una combinación de letras, números y signos de operaciones. Las letras suelen representar cantidades desconocidas y se denominan variables o incógnitas. Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual.
Hay distintos tipos de expresiones algebraicas:
- Dependiendo del número de sumandos, tenemos: monomios (1 sumando) y polinomios (varios sumandos).
- Algunos polinomios tienen nombre propio: binomio (2 sumandos), trinomio (3 sumandos), ...
- Dos expresiones algebraicas separadas por un signo se llama ecuación.
- Un caso particular de ecuación es la identidad, en la que los dos lados de la igualdad son equivalentes.
- Dos expresiones algebraicas separadas por los signos <,>, ≤, ≥ forman una inecuación.
Identidades notables
Hay tres fórmulas que debes conocer. Facilitan las operaciones y te serán de gran ayuda a la hora de simplificar expresiones. Para saber cuáles son y de dónde salen pulsa reproducir en cada una de las escenas.
| Cuadrado de una suma |
Cuadrado de una diferencia |
Suma por diferencia |
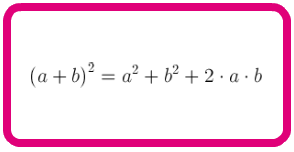 |
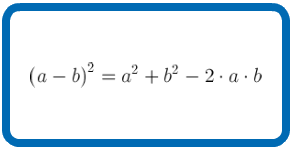 |
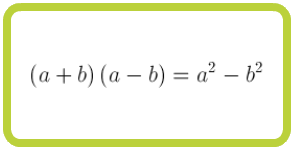 |
Ecuaciones
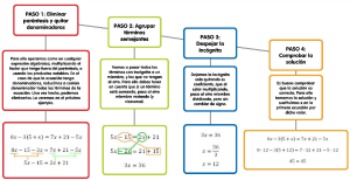
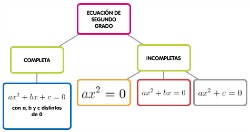
Si pinchas en las imágenes de este apartado descubrirás un resumen de toda la teoría que vimos en el tema 3 sobre ecuaciones de primer y segundo grado. Pero... ¿qué no debemos olvidar sobre esta cuestión?
- La terminología y nomenclatura asociada (grado, coeficiente, incógnita, solución...).
- La técnica para resolverlos en función del tipo de ecuación a la que nos enfrentemos, de primer grado, de segundo grado completa (todos los coeficientes distintos de cero), de segundo grado incompleta...
- El número de soluciones que vamos a obtener en función del tipo de ecuación.
 |
 |
 |
|
Método de resolución ecuación primer grado |
Ecuaciones de segundo grado Haz clic para ampliar |
Inecuaciones
Para resolver una inecuación debes tener presente:
- La solución de una inecuación la forman todos los puntos que cumplen la desigualdad, siempre va a ser un conjunto de puntos, un intervalo o una semirrecta.
- Al sumar o restar la misma cantidad a los dos miembros de una inecuación la desigualdad no varía.
- Al multiplicar o dividir los dos miembros de una inecuación por un mismo número positivo, la desigualdad no varía.
- Al multiplicar o dividir los dos miembros de una inecuación por un mismo número negativo, el sentido de la desigualdad cambia.
Sistemas de ecuaciones lineales
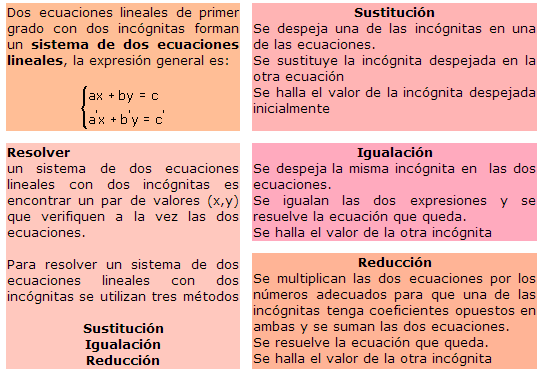 |
| Captura de pantalla del proyecto cidead del Ministerio de Educación |
Un sistema de ecuaciones lineales según su número de soluciones, puede ser:
- Compatible Determinado, si tiene una única solución. Geométricamente, cada una de las ecuaciones representa una recta que se cortan en un único punto.
- Compatible Indeterminado, si tiene infinitas soluciones. Geométricamente, ambas ecuaciones son la misma recta.
- Incompatible, si no tiene solución. Geométricamente, las ecuaciones representan dos rectas paralelas que nunca se cortan.
Caso de estudio
 |
Curso 2010/2011
Halle el conjunto de soluciones de la inecuación:
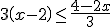
Caso de estudio
 |
Curso 2009/2010
Determine los coeficientes de la ecuación 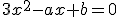 para que sus soluciones sean los valores 3 y -2.
para que sus soluciones sean los valores 3 y -2.