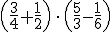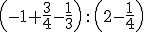1. De los naturales a los racionales
Importante
 |
Pensando en la prueba...
Hasta ahora, en las pruebas realizadas no se han propuesto cuestiones relacionadas exclusivamente con números racionales.
Sin embargo, y de forma implícita sí que han aparecido problemas en los que han sido necesarios utilizar este tipo de números. Por ejemplo, en procesos en los que son necesarios el uso de herramientas de cálculo como pueden ser la regla de Laplace o racionalización.
Por otro lado, en la cabecera de la prueba se menciona: "No olvide que los procesos conducentes a la obtención de resultados deben estar suficientemente justificados".
Por tanto, y debido a la importancia de tener soltura al operar con este tipo de números, se puede considerar "De los naturales a los racionales" como un pilar imprescindible para realizar la prueba con éxito.
 |
| Imagen de elaboración propia |
Clasificación de los números racionales
Si recuerdas en el tema 1 de la primera unidad vimos tres grandes conjuntos numéricos, los racionales que incluían entre ellos a los enteros y a su vez estos incluían los naturales.
- Un número natural es cualquiera de los números que se utilizan para contar un conjunto (recuerda que según quién escriba esta definición, contendrá o no el 0).
- Los números enteros son el conjunto numérico formado por los números naturales y los opuestos de estos, con el 0 siempre incluido. Además, de la clasificación en enteros positivos y en enteros negativos, podemos dividirlos en primos y compuestos en función de sus divisores.
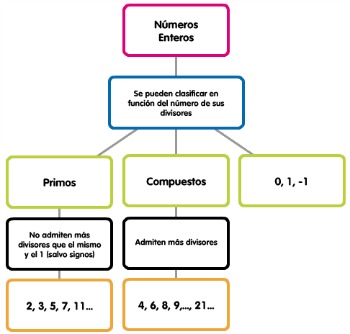 |
| Imagen de elaboración propia. Haz clic para ampliar |
- Por último, decimos que un número es racional si se puede expresar en forma de fracción, es decir, si es el cociente entre dos números enteros. Los números racionales admiten también otra forma de expresión, la decimal, y en función de ella podemos dividir los números racionales en: enteros, exactos (si tiene un número finito de decimales), periódicos puros (si tiene un número infinito de decimales que se repiten) y periódicos mixtos (si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal).
Históricamente la aparición de estos conjuntos numéricos está ligada a las necesidades que le iban surgiendo al hombre. Por ejemplo, el nacimiento de los racionales está íntimamente ligado a la necesidad de dividir la unidad en partes, o la aparición de los enteros a expresar numéricamente acciones como "deber".
Operaciones con números racionales
El plato fuerte de este tema es el desarrollo de destrezas de cálculo con estos conjuntos numéricos. Pero, ¿qué no debemos olvidar?
1. Las distintas operaciones con números. En el caso de la señal de advertencia, ten en cuenta que dependiendo de los elementos que intervengan en la operación, el resultado no tiene porqué pertenecer a ese conjunto numérico. Así por ejemplo, 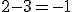 , es decir, que esta resta de números naturales da como resultado un número entero.
, es decir, que esta resta de números naturales da como resultado un número entero.
| Naturales |
Enteros | Racionales |
|
| Suma |
|
|
|
| Resta |
|
|
|
| Multiplicación | |
|
|
| División | |
|
|
| Valor absoluto |
|
||
| Opuesto |
|
|
|
| Potenciación | |
|
|
2. Tener siempre un esquema mental de cómo realizar las operaciones. Por ejemplo para sumar y restar números fraccionarios sin recurrir a la expresión decimal, tenemos que buscar fracciones equivalentes, recurriendo al mínimo común múltiplo.
3. Normalmente, las operaciones vienen combinadas, no aisladas. Por eso el proceso para resolverlas pasa por hacer estas operaciones cada vez más sencillas teniendo en cuenta: la jerarquía, la regla de los signos, la forma de encadenar las operaciones (siempre mediante iguales), las propiedades de las operaciones, y por supuesto sometiéndolas a una comprobación:
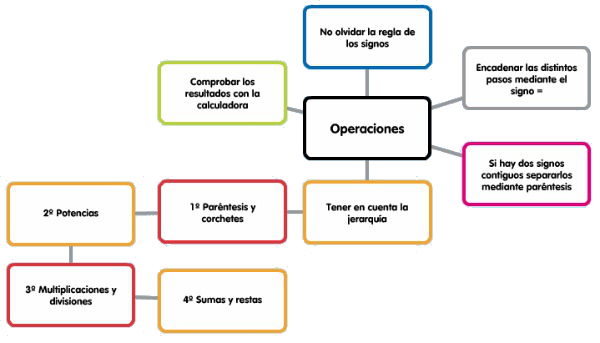 |
| Imagen de elaboración propia |
|
Propiedades suma, resta, multiplicación y división de números racionales por juanmemol
|
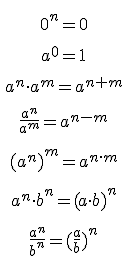 Al trabajar con racionales el exponente tiene que ser entero |
| Propiedades de las potencias |
Ejemplo o ejercicio resuelto
Resuelve las siguientes operaciones:
Caso práctico
 |
Curso 2013/2014
Calcule:
![]()
![]()