3. Estudio energético del campo eléctrico: potencial eléctrico y energía potencial
 |
| Imagen de elaboración propia |
La interacción eléctrica se puede describir también desde el punto de vista energético.
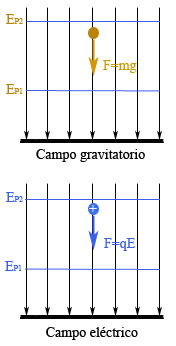
En la Unidad 2 estudiaste que una fuerza, cuando desplaza un cuerpo, realiza un trabajo. Análogamente, si movemos una partícula cargada en contra de un campo eléctrico, realizamos un trabajo.
Pues bien, sabiendo que la fuerza eléctrica es conservativa se puede definir una energía potencial eléctrica, así que si queremos calcular el trabajo necesario para trasladar una carga desde un punto, 1, a otro, 2, en el seno de un campo eléctrico, podremos escribir:
el trabajo realizado por el propio campo será igual a la variación negativa de la energía potencial.
(Recuerda: un cuerpo situado a una cierta altura posee una energía potencial gravitatoria, pues bien, una partícula cargada colocada a una cierta distancia de otra posee una energía potencial eléctrica).
Actividad
La expresión de la energía potencial electrostática en un sistema de dos cargas, Q y q, separadas una distancia r es:
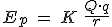
(para llegar a esta expresión se ha debido tomar una referencia: la energía potencial en el infinito es cero (esta es una decisión arbitraria). Si tenemos esto en cuenta, el valor de la energía potencial en cualquier punto se puede hacer calculando la diferencia de energía potencial entre este punto y el infinito.
Así definida, la energía potencial electrostática de una carga eléctrica en un punto es igual al trabajo necesario para traer la carga desde el infinito hasta dicho punto.
A diferencia de lo que ocurría con el campo gravitatorio, el signo de la energía potencial depende del signo relativo de la carga del medio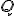 
y de la carga de prueba 
.
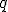- Si ambas cargas tienen el mismo signo, Ep será positiva y las fuerzas del campo no podrán realizar el proceso por ellas mismas, siendo necesario realizar un trabajo para acercar las cargas, que se traducirá en un aumento de la energía potencial electrostática del sistema.
- Si las cargas tienen signo contrario, Ep será negativa y el propio campo realizará el trabajo de traer la carga de prueba, disminuyendo en el proceso la energía potencial electrostática del sistema.
Importante
Actividad
Como la energía potencial eléctrica dependerá de la carga de la partícula, q, es conveniente definir la energía potencial eléctrica por unidad de carga, que recibe el nombre de potencial eléctrico V.
La unidad de potencial en el sistema internacional es el voltio (V). Al potencial eléctrico se le llama también voltaje.
Lo mismo que pasa con la energía potencial eléctrostática, solo podemos conocer diferencias de potencial. Si deseamos establecer el valor del potencial en un punto debemos elegir una referencia (arbitraria) en la que el potencial sea cero. La referencia de nuevo la elegimos en el infinito.
Tal como lo hemos definido, el potencial electrostático en un punto representa el trabajo que realiza la fuerza eléctrica para trasladar la unidad de carga positiva desde ese punto hasta el infinito.
Ejemplo o ejercicio resuelto
 |
| Imagen de elaboración propia |
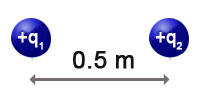
Dos partículas con cargas q1 = 1 μC y q2 = 2 μC están separadas una distancia d = 0,5 m.
Calcula la fuerza que actúa sobre la segunda y su energía potencial electrostática.
 |
| Imagen de elaboración propia |
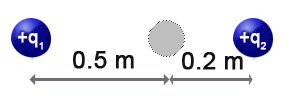
Si q2 puede moverse, partiendo del reposo, ¿hacia dónde lo hará? Si q2 se desplaza por la fuerza electrostática 0,2 m respecto a su posición inicial. ¿Qué trabajo habrá realizado dicha fuerza?
