2.2 Flujo eléctrico
Lo que has visto hasta ahora del campo eléctrico es aquel creado por una carga puntual.
Aunque estrictamente hablando las cargas puntuales no existen, son una idealización útil por varias razones:
- En primer lugar, hay objetos cargados tan pequeños que pueden ser considerados puntuales sin temor a cometer errores significativos. Piensa, por ejemplo, en protones, electrones o iones.
- Por otro lado, los campos eléctricos creados por cuerpos extensos son similares al creado por una carga puntual, siempre y cuando los mires desde una distancia suficientemente grande.
- Por último, el tratamiento matemático de los campos creados por cargas puntuales es... sencillo, como habrás comprobado.
 |
| Imagen de Javier López en INTEF. CC |
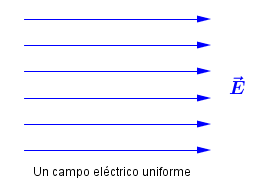
Sin embargo, no todos los campos eléctricos son como el creado por una carga puntual; no todos decrecen con el cuadrado de la distancia ni tienen simetría radial. Por ejemplo, el campo que ves en la imagen es un campo uniforme, tiene el mismo valor en todos los puntos. Este campo no puede ser creado por una carga puntual, pero hay distribuciones de carga que crean campos de este tipo (por cierto, campos muy útiles en la tecnología actual).
Para resolver problemas de campos eléctricos creados por algunas distribuciones de carga, cuando el cuerpo posee un elevado grado de simetría, se trabajará con un teorema matemático facilita enormemente las cosas. Se trata del teorema de Gauss.
Para ello es necesario que conozcas una nueva magnitud física relacionada con los campos. Se trata del concepto de flujo de campo a través de una superficie. Es un concepto muy intuitivo y de gran utilidad, sobre todo para el tema siguiente, cuando estudies el campo magnético.
Importante
El flujo de campo eléctrico a través de una superficie nos da idea del número de líneas de campo que atraviesan dicha superficie perpendicularmente
 |
| Ilustración en INTEF de Javier López . CC |
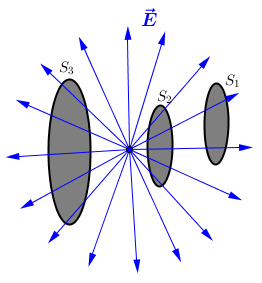
¿De qué dependerá el valor del flujo eléctrico a través de una superficie? La imagen de la izquierda te ayuda a dar respuesta.
El primer factor, el área de la superficie: observa como por la superficie S3 pasan más líneas de campo que por la superficie S1... simplemente por que la superficie es mayor, tiene más área.
El segundo factor depende de la intensidad del campo. Recuerda que las líneas de campo se dibujan de modo que su densidad sea proporcional a la intensidad del campo. Esto significa que cuanto más juntas estén las líneas de campo, mayor será la intensidad de éste. Por esto, aunque las superficies S1 y S2 son iguales (tienen la misma área), el flujo a través de S2 es mayor que a través de S1.
Pero hay algo más...
Reflexión
Vas a analizar las siguientes imágenes. En ellas puedes ver un campo eléctrico uniforme, representado por sus líneas de campo, así como una superficie (rectangular) que está situada en dicho campo y que está orientada de diferente forma en cada imagen.
Piensa cuántas lineas de campo atraviesan perpendicularmente la superficie en cada caso:
 |
|
| Ilustraciones en INTEF, de Javier López, CC | |
 |
|
| Ilustraciones en INTEF, de Javier López. CC | |
Pregunta de Elección Múltiple
Como has podido comprobar, hay otro factor del cual depende el flujo: la orientación relativa entre la superficie y las líneas de campo: El flujo dependerá del ángulo que forme la superficie con el vector intensidad de campo.
Es preciso por ello definir el llamado vector superficie.
Actividad
 |
| Ilustración en INTEF de Javier López. CC |
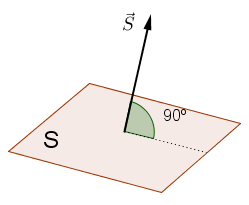
El vector superficie es un segmento orientado cuyo módulo es el área de la superficie y cuya dirección es perpendicular a la misma.
 |
| Ilustración en INTEF de Javier López. CC |
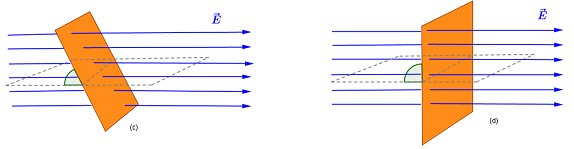
Observando la imagen de la izquierda verás que cuando la superficie es paralela al campo o, dicho de otro modo, cuando el vector superficie es perpendicular al campo, el flujo debe ser cero. Sería la situación mostrada en (a).
Pero cuando la superficie es perpendicular al campo o, dicho de otro modo, cuando el vector superficie es paralelo al campo, el flujo debe ser máximo. Corresponde a la situación de la derecha.
Todo lo que hemos visto hasta ahora concuerda con la expresión matemática que nos permite conocer el flujo:
![]()
Esto es:
![]()
siendo ![]() el ángulo que forman los vectores campo y supeficie.
el ángulo que forman los vectores campo y supeficie.
Importante
El flujo de un campo uniforme a través de una superficie plana se puede calcular como el producto escalar del vector campo por el vector superficie.
![]()
Pregunta de Elección Múltiple
Solution
|
|
|
Ilustración adaptada de Chanchocanen Wikimedia. CC |
Calcular el flujo con la expresión ![]() es solo posible si se cumplen tres condiciones:
es solo posible si se cumplen tres condiciones:
- El módulo del vector intensidad de campo es el mismo en todos los puntos de la superficie.
- La superficie es plana y su área fácil de calcular.
- El ángulo que forman los vectores
 y
y  es el mismo en todos los puntos de la superficie.
es el mismo en todos los puntos de la superficie.
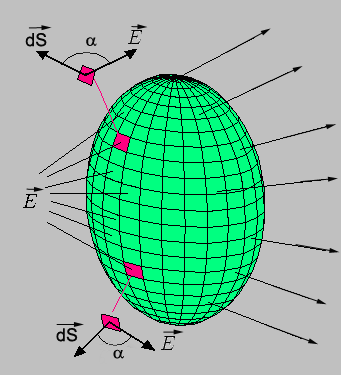
Pero no siempre se darán esas condiciones. ¿Qué hacer entonces? ¿Cómo calcular el flujo en condiciones cualesquiera? Observa la figura: en ella se ilustra una situación general en la que una superficie no plana (en este caso un elipsoide) está inmersa en un campo eléctrico no uniforme (en este caso parece creado por una carga puntual positiva).
En cada punto de la superficie el vector campo es diferente, tanto en módulo como en dirección. Lo mismo sucede con el vector superficie y con el ángulo formado entre ambos vectores. La forma de proceder es la siguiente, muy habitual en Física:
Se divide la superficie en pequeños trocitos, a los que se les conoce como elementos infinitesimales, ![]() , tan pequeños que puedas considerar que, en cada uno de ellos, el vector campo es constante y también lo es el ángulo formado entre
, tan pequeños que puedas considerar que, en cada uno de ellos, el vector campo es constante y también lo es el ángulo formado entre ![]() y
y ![]() . En esas condiciones es posible calcular un elemento infinitesimal de flujo,
. En esas condiciones es posible calcular un elemento infinitesimal de flujo, ![]() .
.
Una vez calculados los elementos infinitesimales de flujo, tan solo hay que sumarlos todos. Esa suma de infinitos elementos infinitesimales de flujo es una integral; en concreto una integral de superficie.
Importante
El flujo de campo eléctrico a través de una superficie cerrada se puede expresar matemáticamente como

Esta integral es, en general, poco amigable. Sin embargo, si se cumplen determinadas condiciones, es muy fácil de resolver. Estas condiciones no son, ni más ni menos, que las enumeradas al principio de este apartado, es decir:
- Que el módulo del vector intensidad de campo sea el mismo en todos los puntos de la superficie S.
- Que el ángulo que forman los vectores
 y
y  sea también el mismo en todos los puntos de la superficie S.
sea también el mismo en todos los puntos de la superficie S.
Si se cumplen estas dos condiciones, la integral se reduce al caso más sencillo: