3. Transformaciones energéticas en el oscilador armónico

Veamos ahora un sistema físico de gran interés: el oscilador armónico.

Recuerda: un oscilador armónico es aquel sistema material que se mueve con movimiento armónico simple.

A continuación se plasmarán aquellas expresiones que nos permitirán determinar cuantitativamente los valores de energías tanto cinética como potencial y, por tanto, de energía mecánica para estos sistemas materiales.

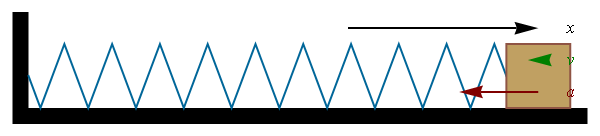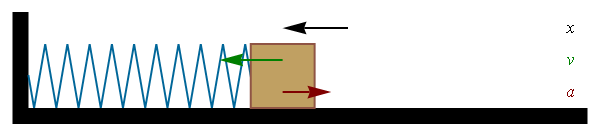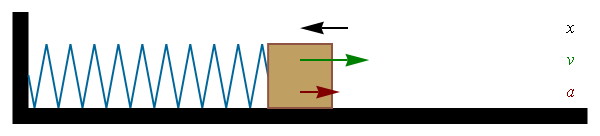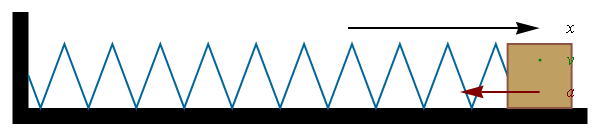Imagen de Gonfer en Wikipedia. CC

Energía cinética

Conocemos la expresión matemática de la energía cinética:

E_{c}= \frac{1}{2}mv^{2}

En ella, puedes observar que la misma depende de la masa del oscilador y de la velocidad que presente el mismo.

Teniendo en cuenta que el valor de la velocidad para un oscilador armónico es:

v=\pm\omega \sqrt{A^{2}-x^{2}}

La energía cinética podrá expresarse como:

E_{c}= \frac{1}{2}m\omega ^{2}(A^{2}-x^{2})

Y por tanto:

\[Ec=\frac{1}{2}K(A^2-x^2)\]

Puedes ver que la energía cinética de un oscilador armónico es una función periódica del tiempo, depende de la elongación y es proporcional a la constante recuperadora del del cuerpo.

Reflexiona

¿En qué puntos será máxima la energía cinética? Realiza una gráfica donde se represente la Ec frente a x.

Energía potencial elástica

Imagen de elaboración propia

Al comprimir o alargar un muelle se realiza trabajo, que queda almacenado en el mismo en forma de energía potencial elástica.

Al igual que ocurría con la energía potencial gravitatoria, el trabajo coincide con el trabajo mecánico necesario para deformar el muelle de la posición inicial a la final, lo que se conoce como elongación del muelle.

Para deformar el muelle es necesario realizar una fuerza F de igual dirección y sentido contrario a la fuerza de restitución del mismo peso (que viene dada por la ley de Hooke que ya estudiaste F=k·x). El valor de la energía potencial elástica resulta ser:

Importante

La energía potencial elástica almacenada en un muelle o resorte toma un valor:

\[Ep_e=\frac{1}{2}kx^2\]

donde k es la constante elástica del muelle y x la elongación (deformación) del mismo.

¿Cómo cambia la energía potencial elástica con la posición?. Observa cómo tendrá un valor mínimo en la posición de equilibrio y un máximo en los extremos.

energía potencial

Caso práctico

Imagen de NIOSH en Wikimedia. CC0

Antes de la irrupción de las balanzas electrónicas, los tenderos utilizaban balanzas como las mostradas en la imagen, cuyo funcionamiento está basado en la deformación de un muelle interno a partir del que es posible calcular el peso colgado.

a) Al instalar una báscula de masa 10 kg el tendero debe colgarla a una altura de 2 metros sobre el suelo, donde se encuentra apoyada. ¿Qué variación ha sufrido la energía potencial gravitatoria del objeto al colocarlo en su nueva posición? ¿Qué trabajo ha debido realizar el tendero para colocarla ahí?

b) Si la constante elástica del muelle es de 2000 N/m y la deformación producida al colgar un objeto es de 15 cm, ¿qué energía potencial elástica habrá almacenado el muelle?

Energía mecánica

Ya has visto la energía cinética y la energía potencial y de qué dependen ambas. Y, como se ha visto en la introducción, la energía mecánica es la suma de ambas energías.

Al realizar la suma de las expresiones se puede calcular la energía mecánica y ver que esta permanece constante a lo largo del tiempo.

En resumen, las expresiones que te permitirán conocer las energías en un movimiento armónico simple son:

En la siguiente animación puedes jugar un poco con los distintos parámetros. Se te mostrarán los valores respectivos para la energía mecánica, cinética y potencial.

Animación de piedrahitapablo en Geogebra.org CC

Importante

Se puede concluir que la energía mecánica del cualquier oscilador permanece constante, siempre y cuando no existan fuerzas disipativas, es decir, aquellas que provocan que el sistema intercambie energía con el exterior. Ejemplos de este último tipo de fuerzas serían las fuerzas de rozamiento o de resistencia.

La energía mecánica es igual al valor máximo de la energía potencial, e igual al valor máximo de la energía cinética. En ningún momento esos valores coinciden para una misma elongación. Por otro lado, la energía mecánica es directamente proporcional al cuadrado tanto de la amplitud como el de la frecuencia que posea el móvil. A lo largo del movimiento, hay una transformación continua de energía potencial en cinética, y viceversa.

Imagen de Javier Carmona del Rio en Wikimedia. CC

Caso práctico

Vídeo de fgarbor906 alojado en Youtube

Imagina un cuerpo, cuya masa es de 3 kg, que se sujeta a un muelle y se hace oscilar con una amplitud de 4 cm y con un período de 2 s.

Determina la energía total del sistema, es decir, la energía mecánica. Piensa si existirá un punto donde la energía cinética y potencial coinciden y si es de esa manera, ¿cuál sería?