2.4 Conservación de la energía mecánica

Tal y como se definió la energía mecánica, podemos dar ahora su expresión desarrollada:

E_m = E_c + E_p = \frac{1}{2}\cdot m \cdot v^2 + m \cdot g\cdot h

Observa la siguiente animación, que reproduce el movimiento de una vagoneta en una montaña rusa:

Grabación de animación de WGBH Educational Foundation autorizada uso educativo

Puedes ver cómo la energía aumenta en el primer trayecto de subida (etapa 1) y desde allí permanece constante, cambiando, eso sí, de tipo, entre el máximo de energía potencial (1) y el máximo de cinética (2), y con puntos intermedios (3), (4), (5) y (6) en los que coexisten ambos tipos de energía, siendo su suma constante e igual a la energía mecánica total del sistema.

En una montaña rusa típica como la descrita, la vagoneta en la que viajamos asciende mediante una cremallera hasta el punto de máxima elevación y, a partir de allí, se deja que describa el circuito sin necesidad de aplicar ningún trabajo sobre ella. En el transcurso de su viaje, puede observarse cómo la velocidad aumenta al descender, disminuyendo al ascender, de forma que la máxima velocidad se presenta en el punto de menor altitud.

Este comportamiento puede explicarse en términos energéticos como una conversión entre las dos

Imagen de elaboración propia

componentes de la energía mecánica: cinética y potencial. Así, en el punto más alto de la trayectoria, su energía cinética es cero y toda la energía está almacenada en forma de energía potencial. Conforme desciende, disminuye la energía potencial y aumenta la energía cinética, al ir adquiriendo progresivamente velocidad. En el punto más bajo de la trayectoria, toda su energía está almacenada como energía cinética.

Si no existieran rozamientos, la vagoneta continuaría indefinidamente su movimiento, ya que no existirían pérdidas energéticas. En la vida cotidiana esto no es cierto, pero como situación idealizada nos permite solucionar problemas complejos con una tasa de error aceptable.

Cuando una magnitud permanece constante, se dice que dicha magnitud se conserva. Este es el caso de la energía mecánica.

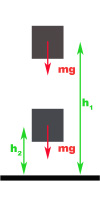
Para comprobarlo, estudiemos el caso de un cuerpo en caída libre desde la posición 1 a la posición 2:

En este caso, si despreciamos el rozamiento con el aire, la única fuerza que actúa sobre el sistema es su peso, y según se ha visto en el apartado 2.3 correspondiente a la energía potencial, podemos escribir:

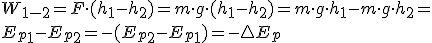
Cabe observar que el signo negativo proviene de que el trabajo realizado por la interacción gravitatoria se utiliza en disminuir su energía potencial.

Por otra parte, según el teorema de las fuerzas vivas, podemos afirmar que

Igualando ambas expresiones, se llega a que:

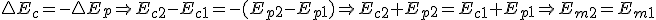
Dicho en otras palabras, la energía mecánica permanece constante, permitiendo expresar el principio de conservación de la energía mecánica:

Importante

La energía mecánica de un sistema aislado permanece constante si no existen rozamientos.

\bigtriangleup E_m = 0 \Rightarrow E_m = cte

Cuando el trabajo de una fuerza sobre un sistema mantiene constante su energía mecánica, indica que dicha fuerza es conservativa.

Caso práctico

Imagen de elaboración propia

Desde una altura de 5 m se deja caer una pelota de 500 g de masa. Suponiendo que no existen rozamientos:

a) ¿Con qué energía cinética llegará al suelo?

b) ¿Con qué velocidad lo hará?

c) Si en vez de la pelota, dejamos caer una piedra de 10 kg, ¿con qué velocidad llegará al suelo?

Comprueba lo aprendido

En una montaña rusa de 25 m de altura máxima, una vagoneta de masa 300 kg se mueve con una velocidad de 10 m/s alpasar por un punto situado a 20 m de altura.

Suponiendo que no existe rozamiento, indica cuáles de las siguientes afirmaciones son correctas:

Retroalimentación

Verdadero

La energía mecánica de la vagoneta es la suma de sus energías cinética y potencial:

E_m= E_c+ E_p = (1/2)·m·v^₂ + m·g·h = (1/2)·300·10² + 300·9.8·20 = 73800 J

Por lo tanto la afirmación es correcta.

Retroalimentación

Falso

Como no existen rozamientos, la energía mecánica se conserva:

ΔE_m= 0 → E_{mi =}E_mf

A nivel del suelo, toda la energía mecánica estará en forma de energía cinética, puesto que la energía potencial vale cero al ser cero la altura. Por lo tanto, como la energía mecánica es de 73800 J (tal y como se ha demostrado en el apartado anterior) resulta:

E_mi=E_mf→ 73800 = (1/2)·m·v^₂ + 0 → v = 22.2 m/s

que será la velocidad que lleve la vagoneta cuando pase a nivel del suelo, y no 20 m/s.

Retroalimentación

Verdadero

De nuevo aplicamos el principio de conservación de la energía mecánica:

ΔE_m= 0 → E_{mi =}E_mf→ 73800 = (1/2)·m·v^₂ + m·g·h = (1/2)·300·v² + 300·9.8·25 →300 = 150·v² →v = 1.4 m/s

Luego la afirmación era verdadera.

2.4 Conservación de la energía mecánica

Importante

Caso práctico

Retroalimentación

Retroalimentación

Retroalimentación

Comprueba lo aprendido

Pregunta 1

Retroalimentación

Pregunta 2

Sugerencia

Retroalimentación

Pregunta 3

Retroalimentación