2.2 Sistemas conservativos
Antes de proseguir en el estudio de la energía mecánica es preciso definir un nuevo concepto: las fuerzas conservativas.
Para ello es imprescindible que recuerdes, del tema anterior, el concepto de trabajo.
Recuerda:
 |
| Imagen en Wikimedia. CC0 |
Se dice que una fuerza es conservativa cuando su trabajo no depende del camino seguido sino que depende únicamente de las posiciones inicial y final.
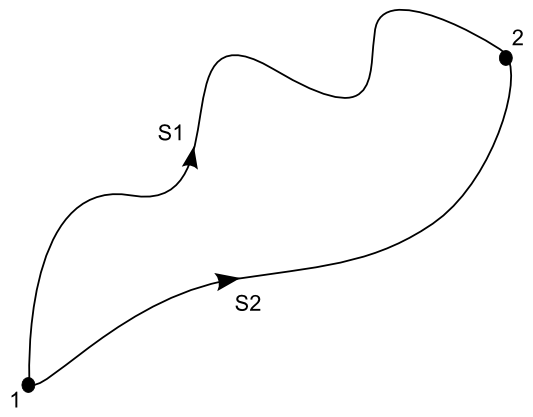
Mira la imagen de la derecha: un cuerpo móvil se desplaza desde el punto 1 hasta el punto 2. Para ello seguirá dos caminos distintos (S1 y S2).
Es lógico que pienses que si el móvil sigue el camino S2, realizará menos trabajo al ser este el camino más corto.
No obstante, se puede comprobar que si la fuerza que hace que el móvil cambie su posición es conservativa, el trabajo desarrollado será el mismo, ya tome un camino u otro.
Este tipo de fuerzas se caracteriza por efectuar un trabajo entre dos puntos que sólo depende de las posiciones de estos, es decir, solo importa el punto de partida y el de llegada, y para nada nos interesa la trayectoria del movimiento.
Importante
Cuando el cuerpo sobre el que actúa una fuerza conservativa se desplaza entre dos posiciones A y B, el trabajo que realiza dicha fuerza es independiente de la trayectoria que recorre el cuerpo. El trabajo realizado por una fuerza conservativa entre dos puntos únicamente depende del punto inicial y del punto final
Según la definición anterior, al trasladarse un cuerpo desde un punto A hasta otro punto B debido a una fuerza conservativa realizamos un trabajo, pero al volver al punto A el trabajo total realizado es cero, es decir, al volver de B a A la fuerza conservativa restituye el trabajo realizado. Así otra posible forma de definir las fuerzas conservativas es:
Las fuerzas conservativas son capaces de restituir todo el trabajo que se realiza para vencerlas.
Piensa un momento cuál será el valor que toma la magnitud trabajo de una fuerza conservativa cuando coinciden el punto inicial y final. Si has pensado que el resultado es cero llevas toda la razón. Se cumple que, hablando de una forma un poco más técnica, la circulación de una fuerza conservativa a través de una trayectoria cerrada toma valor nulo.
\[W_{A\rightarrow A}=\oint F\cdot dr=0\]
Importante
Se denominan fuerzas conservativas las que cumplen que, al actuar sobre una partícula que realiza una trayectoria cerrada, el trabajo realizado es nulo.
Son fuerzas conservativas las fuerzas gravitatoria, elástica y electrostática.
Un aspecto muy importante de las fuerzas conservativas es que estas nos van a permitir definir la energía potencial, que será un número que se asocie a estas fuerzas. Un poco más adelante se aclarará esto.
La situación contraria a este tipo de fuerzas son las fuerzas no conservativas. En este caso, la trayectoria tiene influencia a la hora de establecer la magnitud trabajo. Un ejemplo de estas fuerzas es el rozamiento. Le dedicaremos en este tema un apartado para su estudio.